【算法浅析-0X04】快速排序算法浅析 by arttnba3

0x00 绪论

众所周知，快速排序是所有的排序算法当中速度较快的一种，手撕快排也成为了每一位OIer的必备技能（实际上大部分人都会直接用STL的sort函数XD）
刚好今天ACM选修课布置的课后作业有一道题就是快排模板，所以作为一名不合格的OIer今天来简单讲讲什么是快速排序算法2333

注：这篇文章写于2020.06，只是现在刚刚从CSDN上搬到这里来23333

0x01 基本概念

快速排序（Quick Sort），顾名思义就是很快的排序（大雾），是基于冒泡排序的一种改进的排序算法。

pre.冒泡排序（Bubble Sort）

没学过冒泡排序的可以简单地看一下，学过的直接跳过就行了
顾名思义，数据会“像泡泡一样一个一个冒出水面”，故得名冒泡排序
冒泡排序要对数组进行n-1趟遍历，故时间复杂度为O(N^2)
简单的冒泡排序代码如下：

>void a3_sort(int * array, int n)
>{
>int temp;
>for(int i=0;i<n-1;i++)
   for(int j=0;j<n-1-i;j++)
       if(array[j]>array[j+1])
       {
           temp = array[j];
           array[j] = array[j+1];
           array[j+1] = temp;
       }
>}

基于冒泡排序的思想，C. A. R. Hoare在1960年提出了快速排序算法。

快速排序的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

0x02 原理浅析

快速排序大致可以分为以下几个步骤

step1：选取基准值

在要排序的数组当中选取一个值作为基准值，通常我们可以选array[0]作为基准值，保存在变量key当中

接下来我们需要分别从后向前、从前向后对整个数组进行遍历，故建立变量i=left，j=right（数组始索引与末索引）

step2：从后向前遍历

寻找第一个比key小的值，并将之存在array[i]中

step3：从前向后遍历

寻找第一个比key大的值，并将之存在array[j]中

step4：重复step2、3

直到i>=j，此时整个数组已经被遍历过一遍

要注意的是在step2与step3中已经蕴含了【交换】的过程，故不需要添加而外的交换的语句
也可以理解为step2、3分别找出第一个比key大、小的值，将之进行交换

step5：基准值回归数组，再对其左、右部分进行快排

将数组无限细分下去，一直到所有数据都被排序完毕

想不明白的可以看一看下面的动图

0x03 代码实现

最基础的快速排序的代码实现如下：

void a3_qsort(int* array, int left, int right)
{
    if(left>=right)
        return ;
    int i = left;
    int j = right;
    int key = array[left];
    while(i<j)
    {
        while(i < j && key <= array[j])//从后向前找比key小的
            j--;
        if(i < j)
            array[i++] = array[j];//进行一次交换
        while(i < j && key >= array[i])//从前向后找比key大的
            i++;
        if(i < j)
            array[j--] = array[i];
    }
    array[i] = key;//中间数的回归
    a3_qsort(array, left, i-1);
    a3_qsort(array, i+1, right);
}

0x04 简单优化

“太好🌶，看完以后👴立马就学会了快排”
——“真的🐎？”

实⭐战⭐演⭐练环节不请自来

题目描述
利用快速排序算法将读入的 N 个数从小到大排序后输出。

快速排序是信息学竞赛的必备算法之一。对于快速排序不是很了解的同学可以自行上网查询相关资料，掌握后独立完成。（C++ 选手请不要试图使用STL，虽然你可以使用 sort 一遍过，但是你并没有掌握快速排序算法的精髓。）

输入格式
第1行为一个正整数 N，第2 行包含 N个空格隔开的正整数 ai，为你需要进行排序的数，数据保证了 Ai 不超过 10^9 。

输出格式
将给定的 N个数从小到大输出，数之间空格隔开，行末换行且无空格。

输入输出样例
输入 #1
5 4 2 4 5 1
输出 #1
1 2 4 4 5
说明/提示
对于 20%的数据，有
N≤10^3 ；
对于100% 的数据，有N≤10^5 。
洛谷P1177【模板】快速排序

当你满怀欣喜地将上面的代码复制粘贴进去时，你会发现TLE不请自来…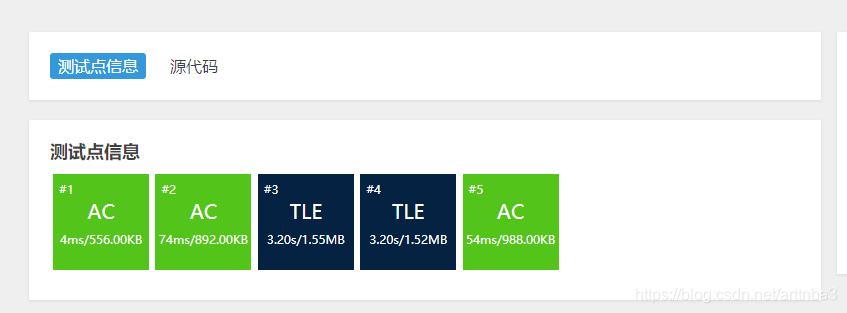

那么我们的问题出在哪呢？（因为写这段代码的人太菜le）

上面的标准化的代码选取的基准是数组的第一个值，在遇到较坏情况时时间复杂度很容易大幅度提高，尤其是在数组有序时，这样的一种分割方式会使快速排序退化为冒泡排序，时间复杂度飙升至O(N^2)

那么最简单的优化方法便是遍历时取位于数组中间的值作为基准值

来自某位大佬的测试结果
最佳的划分是将待排序的序列分成等长的子序列，最佳的状态我们可以使用序列的中间的值，也就是第N/2个数。可是，这很难算出来，并且会明显减慢快速排序的速度。这样的中值的估计可以通过随机选取三个元素并用它们的中值作为枢纽元而得到。事实上，随机性并没有多大的帮助，因此一般的做法是使用左端、右端和中心位置上的三个元素的中值作为枢纽元。显然使用三数中值分割法消除了预排序输入的不好情形，并且减少快排大约14%的比较次数

优化后的代码如下：

void a3_qsort(int* array, int left, int right)
{
    int mid = array[(left+right)/2];//固定以中间的数为基准
    int i = left;
    int j = right;
    do
    {
        while(array[i]<=mid)i++;//从前向后找第一个比mid大的数
        while(array[j]>=mid)j--;//从后向前找第一个比mid小的数
        /*
         * 交换这两个数的位置，使比mid小的数都在mid前面，比mid大的数都在mid后面
         * 注意：在交换过程中mid的位置也是有可能会移动的
         * */
        if(i<=j)
        {
            int temp = array[i];
            array[i] = array[j];
            array[j] = temp;
            i++;
            j--;
        }
    } while (i<=j);//i>j时说明已经遍历过一趟了
    if(left < j)
        a3_qsort(array,left,j);//对j左边的部分进行快排
    if(right > i)
        a3_qsort(array,right,i);//对i右边的部分进行快排
}

结果如下：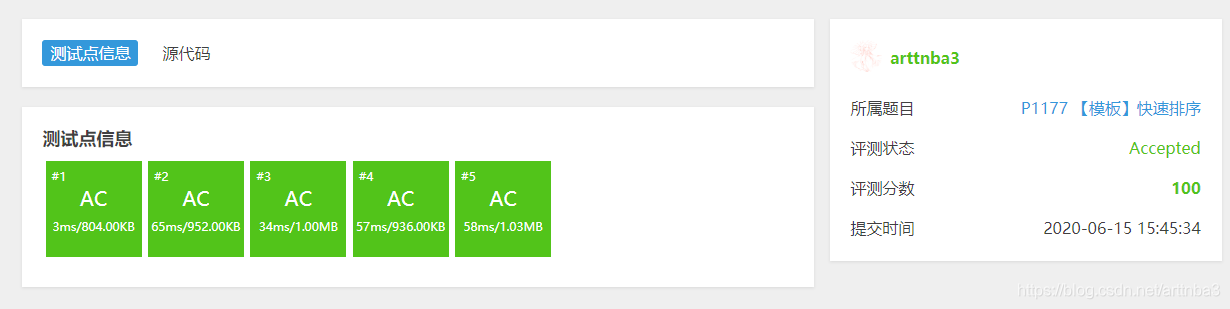

0x05 高级优化

“老师，还有没有更给力点的啊”
——“给👴爪巴”

我们可以看到，上面的这样一种优化虽然可以一定程度上提高快排的效率，但是对于一些糟糕的数据（如很小以及部分有序数组），快排的时间复杂度仍然会飙升

针对这样的情况，我们可以先对数据进行分析，再决定采用什么样的排序方式，多种排序方式混合使用

当然这样子就已经不是纯粹的快排了，但是是不是快排已经无所谓了（误

咕了🕊，后面再把优化补上（👈这个人还在研究STL源码

注：这也是STL中sort()源码的做法