0x00.绪论

为了保持编程的一个手感（毕竟疫情以来打的代码比以前少得多了），同时也为了提高自己的姿势水平（x），打算从今天开始刷Leetcode提供的每日一题并在此做一个小小的记录（x）

希望几年以后这里已经积累了上千道题⑧（~~没可能的~~

0x01. 2020

September

16 - 226. 翻转二叉树（简单）

翻转一棵二叉树。

示例：

输入：
1
2
3
4
5
     4
   /   \
  2     7
 / \   / \
1   3 6   9
输出：
1
2
3
4
5
     4
   /   \
  7     2
 / \   / \
9   6 3   1
备注:
这个问题是受到 Max Howell 的原问题启发的：

谷歌：我们90％的工程师使用您编写的软件(Homebrew)，但是您却无法在面试时在白板上写出翻转二叉树这道题，这太糟糕了。

很常规的也很简单的一道题目，只需逐层交换左右节点即可（~~homebrew的开发者居然写不出这个题么~~（~~估计是太紧张le~~（~~👈不要在意这家伙天天乱讲~~

解法一：递归

一层一层交换结点的做法，我们很容易就想到递归，故构造代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


struct TreeNode* invertTree(struct TreeNode* root)
{
    if(root == NULL)
        return root;
    struct TreeNode * temp;
    temp = root->left;
    root->left = root->right;
    root->right = temp;
    invertTree(root->left);
    invertTree(root->right);
    return root;
}

当然，递归调用会占用大量的栈空间（每次进行函数调用都会生成一个新的栈帧），所以空间复杂度上不是很好看（

解法二：广度优先搜索（队列）

大概过程如下：

头结点入队
交换左右结点
左右结点入队
头结点出队

队列为空时停止即可

因为数据范围不像OI那么变态（x），所以直接用一个很小的数组来储存即可

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


struct TreeNode* invertTree(struct TreeNode* root)
{
    if(root == NULL)
        return root;
    int start=0, end=1;
    struct TreeNode * (queue[1000]), *temp;
    queue[start] = root;
    while(start!=end)
    {
        if(queue[start] != NULL)
        {
            temp = queue[start]->left;
            queue[start]->left = queue[start]->right;
            queue[start]->right = temp;
            queue[end] = queue[start]->left;
            queue[end+1] = queue[start]->right;
            end += 2;
        }
        start++;
    }
    return root;
}

以及这个故事实在是太搞了

17 - 685. 冗余连接 II（困难）

在本问题中，有根树指满足以下条件的有向图。该树只有一个根节点，所有其他节点都是该根节点的后继。每一个节点只有一个父节点，除了根节点没有父节点。

输入一个有向图，该图由一个有着N个节点 (节点值不重复1, 2, …, N) 的树及一条附加的边构成。附加的边的两个顶点包含在1到N中间，这条附加的边不属于树中已存在的边。

结果图是一个以边组成的二维数组。每一个边的元素是一对 [u, v]，用以表示有向图中连接顶点 u 和顶点 v 的边，其中 u 是 v 的一个父节点。

返回一条能删除的边，使得剩下的图是有N个节点的有根树。若有多个答案，返回最后出现在给定二维数组的答案。

示例 1:

输入: [[1,2], [1,3], [2,3]]
输出: [2,3]
解释: 给定的有向图如下:
1
/
v v
2–>3
示例 2:

输入: [[1,2], [2,3], [3,4], [4,1], [1,5]]
输出: [4,1]
解释: 给定的有向图如下:
5 <- 1 -> 2
^ |
| v
4 <- 3
注意:

二维数组大小的在3到1000范围内。
二维数组中的每个整数在1到N之间，其中 N 是二维数组的大小。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/redundant-connection-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

~~第二天就直接上困难难度的题，真有你的啊leetcode~~

~~暂时做不出来，歇菜了Or2~~

解法：并查集

半夜三点多把前置题：684. 冗余连接给做了（见这里），感觉稍微有了点头绪，~~其实还是啥都不知道~~…

晚上大概想清楚了，同样是采用并查集的思想，不过考虑到该图为有向图，同时题目给定的图必定存在一条边使得该图无法成为一颗树

可能存在如下情况：

一个节点的入度大于等于2（存在两个及以上父结点，本题数据构造保证只可能存在两个父结点的情况）
图中存在回路
以上两种情况同时存在

如下图所示（字丑见谅QwQ）：

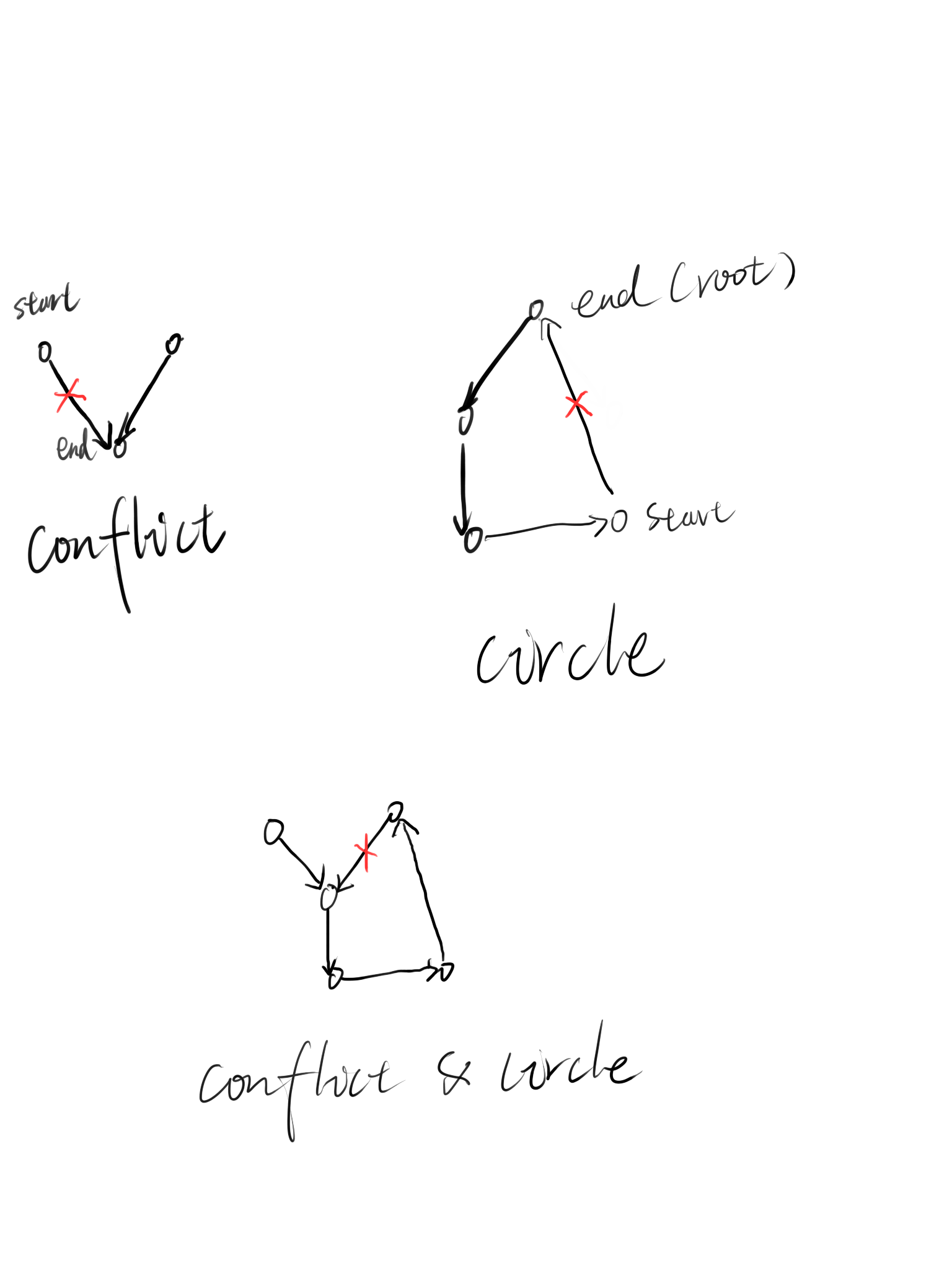
故我们很容易（并不Or2）能够得到解开这道题的算法：

将每一个结点初始化为一棵单独的树，其父结点初始化为自身
使用两个数组分别保存每个结点的父结点与所属的树的根结点
遍历每一条边，重新记录下每个结点的父结点与根节点
当一个结点的入度大于1时，记录该边为争议边
当一条边的始末结点同属于一棵树时，记录该条边为回路边
两种情况都不存在，则将该边的末结点的父结点标为该边的始结点，并合并两结点所在的树
当争议边不存在时，直接删除回路边
争议边若存在，若同时存在回路边，则删除争议边末尾结点及其父结点所构成边，否则删除争议边

构造代码如下：

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
 /**
 * Note: The returned array must be malloced, assume caller calls free().
 */

int * ancestors;//记录每个节点的根结点
int * parent;//记录每个节点的父结点

int find_x(int x)
{
    return x == ancestors[x] ? x : (ancestors[x] = find_x(ancestors[x]));//路径压缩
}

void union_ancestor(int a, int b)
{
    ancestors[find_x(a)] = find_x(b);//将两棵树合并为一棵树
}

int* findRedundantDirectedConnection(int** edges, int edgesSize, int* edgesColSize, int* returnSize)
{    
    ancestors = (int*)malloc(sizeof(int)*(edgesSize+5));
    parent = (int*)malloc(sizeof(int)*(edgesSize+5));

    for(int i=1;i<=edgesSize;i++)
    {
        parent[i] = ancestors[i] = i;//初始化每个结点为单独的一棵树（并查集），结点的父结点标记为自身
    }
	//conflict：可能存在争议的边
    //circle：可能形成回路的边
    int start, end, a_start, a_end, conflict = -1, circle = -1;

    for(int i=0;i<edgesSize;i++)
    {
        start = edges[i][0];
        end = edges[i][1];
        a_start = find_x(start);
        a_end = find_x(end);
        if(parent[end] != end)//该条边的尾结点已经与其他结点相连（即加上这条边后入度大于1）
        {
            conflict = i;
        }
        else
        {
            parent[end] = start;
            if(a_start == a_end)
            {
                circle = i;//该条边两结点的根结点相同，可能形成回路
            }
            else
            {
                union_ancestor(start, end);//将两棵树合并为一棵树（并查集）
            }
        }
    }

    int *ret = (int*)malloc(sizeof(int)*2);
    *returnSize = 2;
    if(conflict<0)//不存在争议边，只存在形成回路的边
    {
        ret[0] = edges[circle][0];
        ret[1] = edges[circle][1];
        return ret;
    }
    else//存在争议边
    {
        if(circle>0)//同时存在回路边
        {
            ret[0] = parent[edges[conflict][1]];
            ret[1] = edges[conflict][1];
            return ret;
        }
        else
        {
            ret[0] = edges[conflict][0];
            ret[1] = edges[conflict][1];
            return ret;
        }
    }
    return ret;
}

18 - 47. 全排列 II（中等）

明早起来再看，先咕咕咕了（

19 - 404. 左叶子之和（简单）

计算给定二叉树的所有左叶子之和。

示例：
3
/ \
9 20
/ \
15 7

在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/sum-of-left-leaves
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解法一：深度优先搜索（DFS）

一层一层地搜下去，若左结点为叶子结点（无子女）则加上左结点的值，否则搜索子结点，若右结点不为子结点则搜索右结点的子节点

得代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

bool isLeaf(struct TreeNode * root)
{
    return !root->left && !root->right;
}

int dfs(struct TreeNode* root)
{
    int ans = 0;
    ans += root->left ? (isLeaf(root->left) ? root->left->val : dfs(root->left)) : 0;
    ans += (root->right!=NULL&&!isLeaf(root->right)) ? dfs(root->right) : 0;
    return ans;
}

int sumOfLeftLeaves(struct TreeNode* root)
{
    return root ? dfs(root) : 0;
}

//利用三目运算符的一行流
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

int sumOfLeftLeaves(struct TreeNode* root)
{
    return root ? (root->left && !root->left->left && !root->left->right ? root->left->val + sumOfLeftLeaves(root->right) : sumOfLeftLeaves(root->left)+sumOfLeftLeaves(root->right)) : 0;
}

解法二：广度优先搜索（BFS）+ 队列

这个解法是从官方的题解上看来的

使用队列数据结构来实现广度优先搜索

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

bool isLeafNode(struct TreeNode *node) 
{
    return !node->left && !node->right;
}

int sumOfLeftLeaves(struct TreeNode *root) 
{
    if (!root) 
    {
        return 0;
    }
    struct TreeNode **q = malloc(sizeof(struct TreeNode *) * 1001);
    int left = 0, right = 0;
    q[right++] = root;
    int ans = 0;
    while (left < right) 
    {
        struct TreeNode *node = q[left++];
        if (node->left) 
        {
            if (isLeafNode(node->left)) 
            {
                ans += node->left->val;
            } 
            else 
            {
                q[right++] = node->left;
            }
        }
        if (node->right) 
        {
            if (!isLeafNode(node->right)) 
            {
                q[right++] = node->right;
            }
        }
    }
    return ans;
}

当然，这么做有一个缺点就是需要提前开辟较大的空间

20 - 78. 子集（中等）

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/subsets
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

本题要求我们返回一个数组中的所有元素所组成的集合的所有子集（包括空集）

解法：迭代法遍历数组

考虑到二进制数的特殊性质（000→001→010→011→100→101→110→111），我们使用二进制数的每一位来表示是否选取数组中的该位数可以很方便地遍历完所有选取的情况

如下图所示

同时由二项式定理可知一共有2^n种情况（x=1）

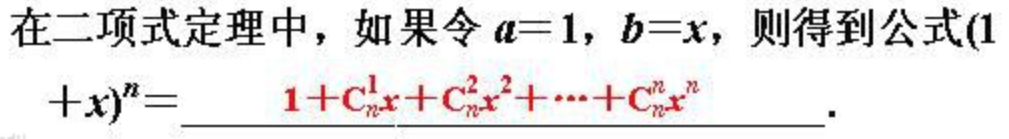
故构造代码如下：

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
int** subsets(int* nums, int numsSize, int* returnSize, int** returnColumnSizes) 
{
    int amount = (1 << numsSize);
    int **retn = (int**)malloc(sizeof(int*)*amount);
    *returnSize = amount;
    *returnColumnSizes = (int*)malloc(sizeof(int)*amount);
    int set[numsSize];
    for(int i=0;i<amount;i++)
    {
        int n = 0;
        for(int j=0;j<numsSize;j++)
        {
            if(i & (1 << j))
            {
                set[n++] = nums[j];
            }
        }
        int *temp = (int*)malloc(sizeof(int)*n);
        memcpy(temp,set,sizeof(int)*n);
        (*returnColumnSizes)[i] = n;//踩坑点
        retn[i] = temp;
    }
    return retn;
}

需要注意的是二级指针的概念和使用方法

~~以及我想不通为什么returnColumnSizes要用二级指针~~

21 - 538. 把二叉搜索树转换为累加树（简单）

给定一个二叉搜索树（Binary Search Tree），把它转换成为累加树（Greater Tree)，使得每个节点的值是原来的节点值加上所有大于它的节点值之和。

例如：

输入: 原始二叉搜索树:
5
/
2 13

输出: 转换为累加树:
18
/
20 13

注意：本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/convert-bst-to-greater-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

二叉搜索树有一个特点就是结点左子树的结点都比该结点小，右子树的结点都比该结点大，因而叫二叉搜索树，可以用以大幅缩短搜索的时间

解法：深度优先搜索 + 反序中序遍历

由于二叉查找树的这个特性，我们考虑递归实现的深度优先搜索算法，通过反序中序遍历来实现，过程如下：

遍历右子树，将右子树结点值加到summary
将当前结点值加到summary
将当前结点值置为summary
遍历左子树

每个结点需要一个额外的栈空间，因而空间复杂度为O(N)；需要遍历每个结点一次，因而时间复杂度为O(N)

构造代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


void dfs(struct TreeNode* root, int *sum)
{
    if(!root)
        return;
    dfs(root->right,sum);
    *sum+=root->val;
    root->val=*sum;
    dfs(root->left,sum);
    return;
}

struct TreeNode* convertBST(struct TreeNode* root)
{
    int sum = 0;
    dfs(root, &sum);
    return root;
}

22 - 968. 监控二叉树（困难）

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

示例 1：

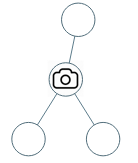
输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。
示例 2：

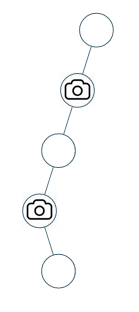
输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。上图显示了摄像头放置的有效位置之一。

提示：

给定树的节点数的范围是 [1, 1000]。
每个节点的值都是 0。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/binary-tree-cameras
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

~~又是hard，真有你的啊leetcode~~

仔细想想，对于一个结点是否需要安装摄像头，其实是由其子树的状态来决定的，那么我们可以使用动态规划算法

解法：递归 + 深度优先搜索（DFS） + 动态规划（DP）

大概如下图所示：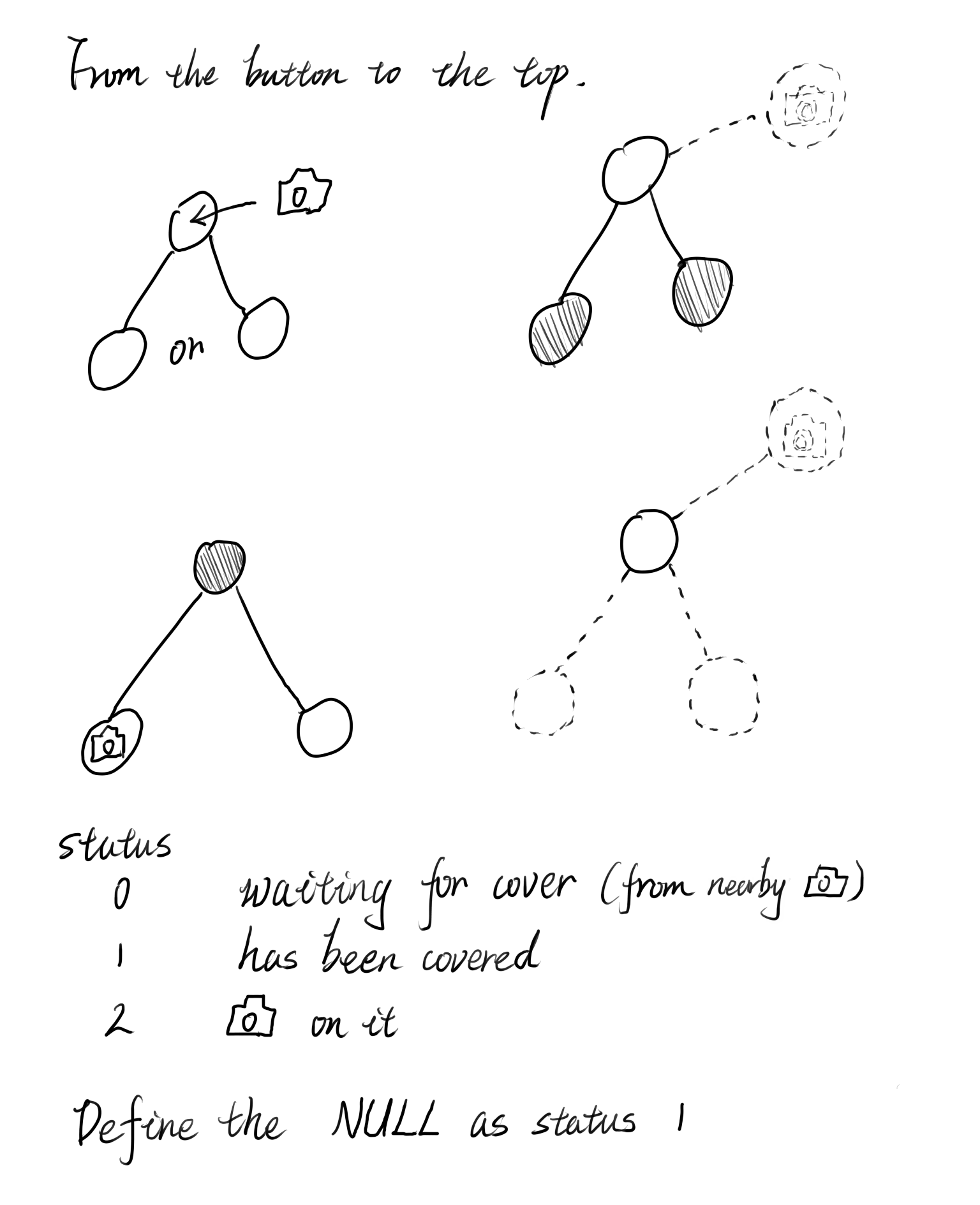

我们考虑有以下几种情况：

当一个结点的左或右子树没有被摄像头覆盖上时，这个结点必须要安装一个摄像头来监测其左或右子树，定义为状态码STATUS_CAMERA
当一个结点的左右子树都已经被摄像头覆盖上时，为了实现摄像头数量的最小化，需要在该结点的父结点放置摄像头，即在回到父结点前该结点都是未被覆盖的，定义为状态码STATUS_UNCOVERED
当一个结点的左右子树中存在摄像头，则该结点肯定是被覆盖了的，定义为状态码STATUS_COVERED
对于结点为NULL的情况，我们可以默认他是被覆盖了的结点，即定义为状态码STATUS_COVERED

同时，我们还需要对这棵树的根节点做一次单独的检测，以确定是否要在其上放置摄像头

为了方便判定，我们将STATUS_CAMERA设置为状态码中值相对大的一个

状态转移方程

STATUS_ROOT = F(STATUS_LEFT, STATUS_RIGHT)

时间复杂度：

n次遍历，线性时间复杂度O(N)

空间复杂度：

递归算法要开辟n个栈空间，故为线性空间复杂度O(N)

构造代码如下：

C语言版

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

/*
 * status code
 * 0: waiting for pwn
 * 1: has been pwn
 * 2: camara here
 *-1: inner error, just a placeholder in fact
 */
#define STATUS_UNCOVERED 0
#define STATUS_COVERED 1
#define STATUS_CAMERA 2
#define STATUS_ERROR -1

int minCameraCover(struct TreeNode* root) 
{
    int amounts=0;//amounts of camera

    //add a camera to the root if status of root is 0
    if(dfs(root,&amounts) == STATUS_UNCOVERED)
        amounts++;
    return amounts;
}

int dfs(struct TreeNode* root, int * amounts)
{
    //NULL pointer signed as status 1
    if(!root)
        return STATUS_COVERED;

    //get the status of left and right node
    int left = dfs(root->left, amounts);
    int right = dfs(root->right, amounts);

    //if one of both uncovered yet, a camera is needed
    if(left == STATUS_UNCOVERED || right == STATUS_UNCOVERED)
    {
        (*amounts)++;
        return STATUS_CAMERA;
    }

    //if both are covered, father's of root may need a camera
    if(left == STATUS_COVERED && right == STATUS_COVERED)
        return STATUS_UNCOVERED;
    
    //if there's at least one camera in both childs, the root is covered
    if(left + right > STATUS_CAMERA)
        return STATUS_COVERED;
    
    //error code(not used)
    return STATUS_ERROR;
}

Python语言版：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

#  status
#  0 - waiting for pwn
#  1 - has been pwn
#  2 - camera here
# -1 - error, just a placeholder

class Solution:
    amounts = 0

    def dfs(self, root: TreeNode) -> int:
        if root == None:
            return 1
        left = self.dfs(root.left)
        right = self.dfs(root.right)
        if left == 1 and right == 1:
            return 0
        if left == 0 or right == 0:
            self.amounts += 1
            return 2
        if left + right > 2:
            return 1
        return -1

    def minCameraCover(self, root: TreeNode) -> int:
        if self.dfs(root) == 0:
            self.amounts += 1
        return self.amounts

23 - 617. 合并二叉树（简单）

给定两个二叉树，想象当你将它们中的一个覆盖到另一个上时，两个二叉树的一些节点便会重叠。

你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠，那么将他们的值相加作为节点合并后的新值，否则不为 NULL 的节点将直接作为新二叉树的节点。

示例 1:

输入:
Tree 1 Tree 2
1 2
/ \ / \
3 2 1 3
/ \ \
5 4 7
输出:
合并后的树:
3
/ \
4 5
/ \ \
5 4 7
注意: 合并必须从两个树的根节点开始。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/merge-two-binary-trees
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

很简单的一道题，~~3分钟不到就做出来了，今晚可以做个好梦了~~（确信

解法：递归 + 深度优先搜索（DFS）

逐层递归，合并到t1上：

t1、t2若为空则直接返回其中非空的那一个
将t2的val加到t1的val上
合并t1左与t2左
合并t1右与t2右

得到代码如下：

时间复杂度：

搜索的次数和结点数量线性增长，故时间复杂度为O(N)

空间复杂度：

需要的栈空间数量和结点数量线性增长，故空间复杂度为O(N)

C语言版：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


struct TreeNode* mergeTrees(struct TreeNode* t1, struct TreeNode* t2)
{
    if(!t1)
        return t2;
    if(!t2)
        return t1;
    t1->val += t2->val;
    t1->left = mergeTrees(t1->left,t2->left);
    t1->right = mergeTrees(t1->right,t2->right);
    return t1;
}

Python语言版：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def mergeTrees(self, t1: TreeNode, t2: TreeNode) -> TreeNode:
        if t1 == None:
            return t2
        if t2 == None:
            return t1
        t1.val += t2.val
        t1.left = self.mergeTrees(t1.left, t2.left)
        t1.right = self.mergeTrees(t1.right, t2.right)
        return t1

24 - 501. 二叉搜索树中的众数（简单）

给定一个有相同值的二叉搜索树（BST），找出 BST 中的所有众数（出现频率最高的元素）。

假定 BST 有如下定义：

结点左子树中所含结点的值小于等于当前结点的值
结点右子树中所含结点的值大于等于当前结点的值
左子树和右子树都是二叉搜索树
例如：
给定 BST [1,null,2,2],

1
\
2
/
2
返回[2].

提示：如果众数超过1个，不需考虑输出顺序

进阶：你可以不使用额外的空间吗？（假设由递归产生的隐式调用栈的开销不被计算在内）

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/find-mode-in-binary-search-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解法：递归 + 深度优先搜索（DFS）

考虑到二叉搜索树中左子树所有结点的值小于当前结点值小于右子树所有结点的值，故还是采取深度优先搜索算法

递归中序遍历，由于二叉搜索树的特殊性质，我们遍历的顺序一定是排序好的

故构造代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


/**
 * Note: The returned array must be malloced, assume caller calls free().
 */

int max;//数量最多的数的数量
int num;//前一结点的连续结点个数
int pre;//前一结点的值
int size;//返回的数组的大小
int *retn;//返回的数组

int* findMode(struct TreeNode* root, int* returnSize)
{
    retn = (int*)malloc(sizeof(int)*2150);
    if(!root)
    {
        *returnSize = 0;
        return retn;
    }
    max = 0;
    pre = 0xdeadbeef;
    size = 0;
    num = 0;
    dfs(root);
    *returnSize = size;
    return retn;
}

void dfs(struct TreeNode * root)
{
    if(!root)
        return;
    dfs(root->left);

    if(root->val == pre)
        num++;
    else//新序列
        num = 1;
    
    if(num > max)//相同结点数量比max还多，则进行重置
    {
        size = 0;
        retn[size++] = root->val;
        max = num;
    }
    else if(num == max)//否则，放入数组中
    {
        retn[size++] = root->val;        
    }

    pre = root->val;//储存该结点值，继续遍历下一结点

    dfs(root->right);
    
}

25 - 106. 从中序与后序遍历序列构造二叉树（中等）

根据一棵树的中序遍历与后序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]
返回如下的二叉树：
    3

/ \\
9 20
/ \
15 7

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

~~一上来就把我给看懵了，真有你的啊leetcode~~

解法：递归

这道题主要的突破点是后序遍历所得的数组

中序遍历的顺序是：根->左->右

后序遍历的顺序是：左->右->根

也就是说，后序遍历的最后一个结点必定是这一棵树的根结点，而中序遍历所得的结果中根结点的左边所有结点必定属于左子树，右边所有结点必定属于右子树

在后序列表中，前left个值为左子树，left+1到left+right为右子树；
在中序列表中，根结点前为左子树，根结点后为右子树；

依照这个性质，我们便可以按照中序遍历的顺序重构这一棵树

构造代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


struct TreeNode* buildTree(int* inorder, int inorderSize, int* postorder, int postorderSize)
{
    if(!inorderSize || !postorderSize)
        return NULL;
    
    struct TreeNode * node = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    int root = postorder[postorderSize-1];
    
    node->val = root;
    int left;
    for(left = 0;left<inorderSize;left++)
        if(inorder[left] == root)
            	break;
    
    int right = inorderSize - left - 1;
    
    node->left = buildTree(inorder, left, postorder, left);
    node->right = buildTree(inorder + left + 1, right, postorder + left, right);

    return node;
}

26 - 113. 路径总和 II（中等）

给定一个二叉树和一个目标和，找到所有从根节点到叶子节点路径总和等于给定目标和的路径。

说明: 叶子节点是指没有子节点的节点。

示例:
给定如下二叉树，以及目标和 sum = 22，
          5
         / \\
        4   8
       /   / \\
      11  13  4
     /  \\    / \\
    7    2  5   1
返回:

[
[5,4,11,2],
[5,8,4,5]
]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/path-sum-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解法：深度优先搜索（DFS）+ 递归中序遍历

中序遍历，一层一层地搜下去就完事了，用一个栈来保存路径，遇到叶子结点且刚好到了这一层时sum已经被减到0了就保存路径

需要注意的是在每一层搜索结束后都要将该层结点弹出栈

构造代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
int **retn;
int *set;
int nums;
int retn_nums;

void dfs(struct TreeNode* root, int sum, int** returnColumnSizes)
{
    if(!root)
        return;
    
    sum -= root->val;
    set[nums++] = root->val;

    if(!root->left && !root->right && !sum)
    {
        int * path = (int*) malloc(sizeof(int) * nums);
        memcpy(path, set, sizeof(int) * nums);
        (*returnColumnSizes)[retn_nums] = nums;
        retn[retn_nums++] = path;
    }

    dfs(root->left,sum,returnColumnSizes);
    dfs(root->right,sum,returnColumnSizes);
    nums--;
}

int** pathSum(struct TreeNode* root, int sum, int* returnSize, int** returnColumnSizes)
{
    retn_nums = nums = 0;
    set = (int*) malloc(sizeof(int)*1000);
    retn = (int**)calloc(1000,sizeof(int*));
    if(!root)
    {
        *returnSize = 0;
        (*returnColumnSizes)[0] = 0;
        return NULL;
    }
    dfs(root,sum,returnColumnSizes);
    *returnSize = retn_nums;
    return retn;
}

27 - 235. 二叉搜索树的最近公共祖先（简单）

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-search-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解法：深度优先搜索（DFS）

二叉搜索树（BST）有一个很重要的性质就是左子树所有结点都小于当前节点，右子树所有结点都大于当前结点，所以我们可以直接通过比较结点的值来进行判断

构造代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

struct TreeNode* lowestCommonAncestor(struct TreeNode* root, struct TreeNode* p, struct TreeNode* q) 
{
    if(p == q)
        return p;
    
    bool flag1 = p->val > root->val;
    bool flag2 = q->val > root->val;
    if(flag1 != flag2)
        return root;
    
    if(p == root || q == root)
        return root;

    if(flag1)
        return lowestCommonAncestor(root->right,p,q);

    return lowestCommonAncestor(root->left,p,q);
}

早睡早起身体好（确信

28 - 117. 填充每个节点的下一个右侧节点指针 II（中等）

给定一个二叉树

struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

进阶：

你只能使用常量级额外空间。
使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

示例：

输入：root = [1,2,3,4,5,null,7]
输出：[1,#,2,3,#,4,5,7,#]
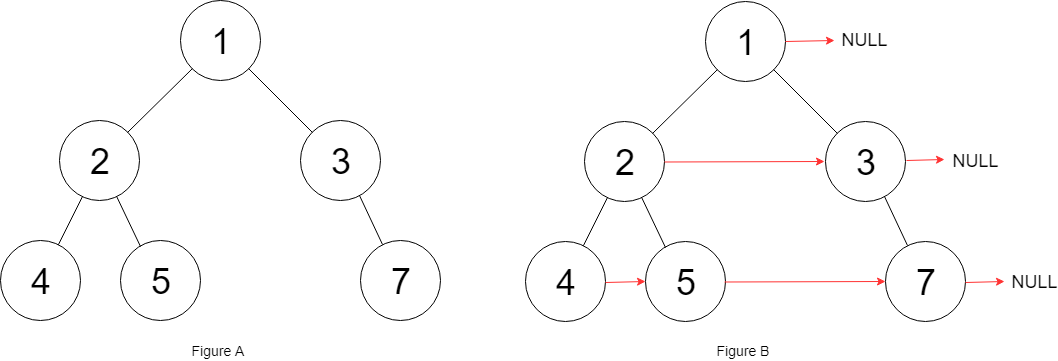
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。

提示：

树中的节点数小于 6000
-100 <= node.val <= 100

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/populating-next-right-pointers-in-each-node-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解法一：层次遍历

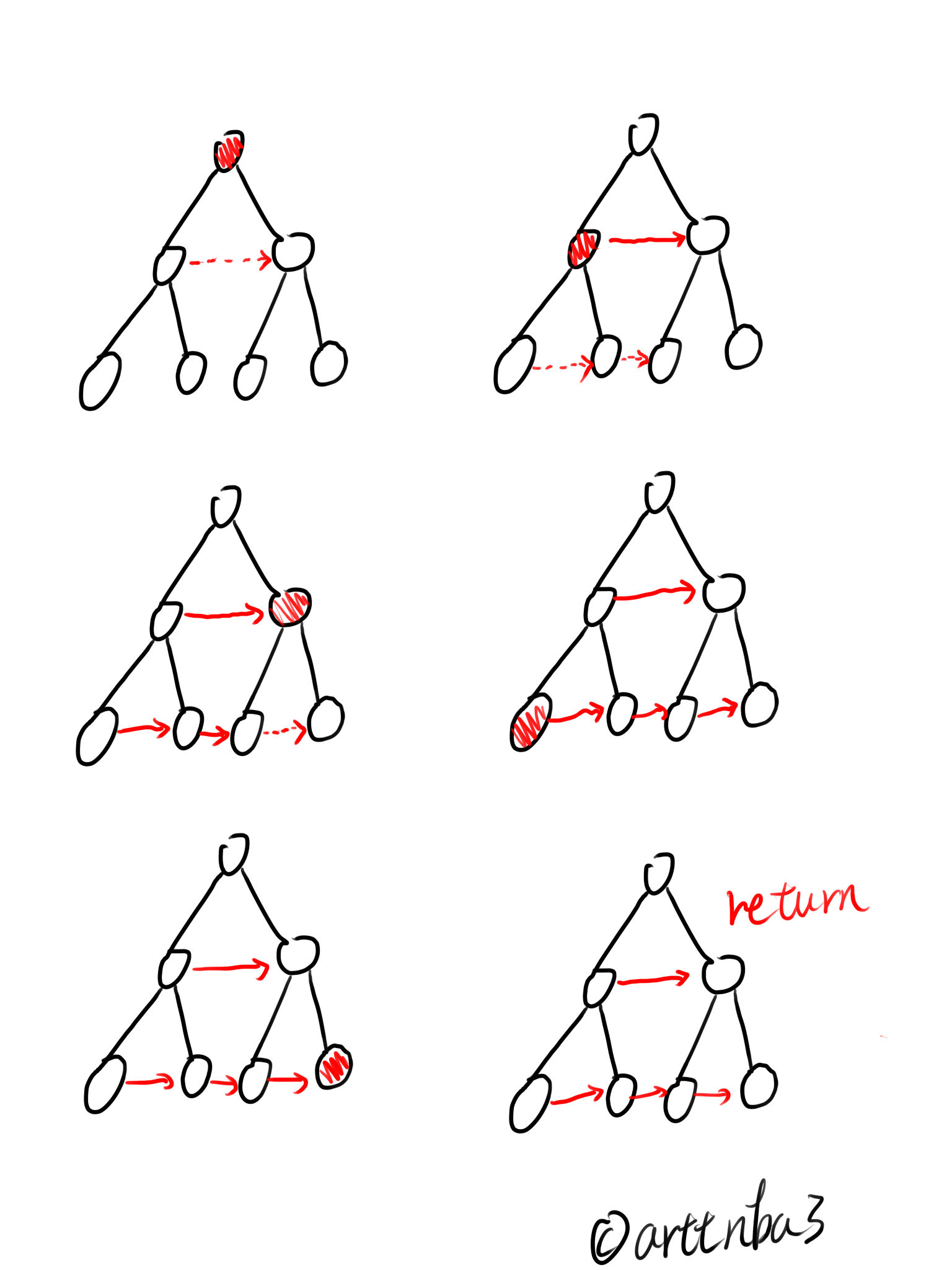
我们考虑到当我们填充next指针将每一层的结点都连接起来后，该层所有结点便构成了一个单向链表，我们可以通过遍历每一层的链表来构造下一层的链表

大致过程如下图

时间复杂度：

由于每个结点都要遍历一次，故时间复杂度为O(N)

空间复杂度：

由于没有使用到额外的空间，故空间复杂度为O(1)

C语言版：

我么可以得到如下代码：

/**
 * Definition for a Node.
 * struct Node {
 *     int val;
 *     struct Node *left;
 *     struct Node *right;
 *     struct Node *next;
 * };
 */

struct Node * last_node, *next_start;

void connectList(struct Node * node)
{
    if(last_node)
    {
        last_node->next = node;
    }
    if(!next_start)
    {
        next_start = node;
    }
    last_node = node;
}

struct Node *connect(struct Node *root) 
{
    if (!root)
        return NULL;

    struct Node *start = root;
    while(start)
    {
        last_node = NULL, next_start = NULL;
        while(start)
        {
            if(start->left)
                connectList(start->left);
            if(start->right)
                connectList(start->right);
            start = start->next;
        }
        start = next_start;
    }
    return root;
}

Python语言版：

"""
# Definition for a Node.
class Node:
    def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
        self.val = val
        self.left = left
        self.right = right
        self.next = next
"""

class Solution:
    def __init__(self):
        self.last_node: 'Node'
        self.next_start: 'Node'


    def connect(self, root: 'Node') -> 'Node':
        if root == None:
            return root

        start = root

        while start != None:
            self.last_node = None
            self.next_start = None

            while start != None:
                if start.left != None:
                    if self.last_node != None:
                        self.last_node.next = start.left

                    if self.next_start == None:
                        self.next_start = start.left

                    self.last_node = start.left

                if start.right != None:
                    if self.last_node != None:
                        self.last_node.next = start.right

                    if self.next_start == None:
                        self.next_start = start.right

                    self.last_node = start.right

                start = start.next

            start = self.next_start
        
        return root
                


    def connectList(self, node: 'Node'):

        if self.last_node != None:
            self.last_node.next = node

        if self.next_start == None:
            self.next_start = node

        self.last_node = node

![XTJUK27UN3_66_OSL5`_BZB.png](https://i.loli.net/2020/09/28/ywXFL85CP4Zm2B6.png)

29 - 145. 二叉树的后序遍历（中等）

给定一个二叉树，返回它的后序遍历。

示例:

输入: [1,null,2,3]
1

2
/
3

输出: [3,2,1]
进阶: 递归算法很简单，你可以通过迭代算法完成吗？

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/binary-tree-postorder-traversal
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解法一：深度优先搜索（DFS） + 递归后续遍历

后序遍历的顺序是左→右→根，使用递归可以三分钟内解决

时间复杂度：

每个结点都过一遍，所以时间复杂度是O(N)

空间复杂度：

每个结点都要开辟一个单独的栈帧空间，故空间复杂度为O(N)

构造代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int * retn;
int size;
void dfs(struct TreeNode* root)
{
    if(!root)
        return;

    if(root->left)
        dfs(root->left);
    
    if(root->right)
        dfs(root->right);

    retn[size++] = root->val;
}

int* postorderTraversal(struct TreeNode* root, int* returnSize)
{
    
    if(!root)
    {
        *returnSize = 0;
        return NULL;
    }
    retn = (int*) malloc(sizeof(int)*1000);
    size = 0;

    dfs(root);
    *returnSize = size;

    return retn;
}

30 - 701. 二叉搜索树中的插入操作（中等）

给定二叉搜索树（BST）的根节点和要插入树中的值，将值插入二叉搜索树。返回插入后二叉搜索树的根节点。输入数据保证，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。你可以返回任意有效的结果。

例如,

给定二叉搜索树:
    4
   / \
  2   7
 / \
1   3
和插入的值: 5
你可以返回这个二叉搜索树:
     4
   /   \
  2     7
 / \   /
1   3 5
或者这个树也是有效的:
     5
   /   \
  2     7
 / \   
1   3
     \
      4
提示：

给定的树上的节点数介于 0 和 10^4 之间
每个节点都有一个唯一整数值，取值范围从 0 到 10^8
-10^8 <= val <= 10^8
新值和原始二叉搜索树中的任意节点值都不同

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/insert-into-a-binary-search-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解法：深度优先搜索（DFS）

深度优先搜索遍历这棵树， 插入值大于结点值则往右子树插，否则往左子树插

递归可以很方便地解决这个问题

时间复杂度：

每个结点都有可能过一遍，所以时间复杂度是O(N)

空间复杂度：

每个结点都要开辟一个单独的栈帧空间，故空间复杂度为O(N)

构造代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
void dfs(struct TreeNode* root, int val)
{
    if(!root)
        return;

    if(val > root->val)
    {
        if(!root->right)
        {
            root->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));
            root->right->val = val;
            root->right->left = NULL;
            root->right->right = NULL;
        }
        else
        {
            dfs(root->right, val);
        }
    }
    else
    {
        if(!root->left)
        {
            root->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));
            root->left->val = val;
            root->left->left = NULL;
            root->left->right = NULL;
        }
        else
        {
            dfs(root->left, val);
        }
    }
}

struct TreeNode* insertIntoBST(struct TreeNode* root, int val)
{
    if(!root)
    {
        root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
        root->left = NULL;
        root->right = NULL;
        root->val = val;
        return root;
    }
    dfs(root, val);
    return root;
}

![Z08G_KN_4GTD1`J_3NC0__F.png](https://i.loli.net/2020/09/30/EUIqglNFiRvJCoz.png)

又是能够早睡的一个晚上（确信

九月结束🌶

October

1 - LCP 19. 秋叶收藏集（中等）

小扣出去秋游，途中收集了一些红叶和黄叶，他利用这些叶子初步整理了一份秋叶收藏集 leaves，字符串 leaves 仅包含小写字符 r 和 y，其中字符 r 表示一片红叶，字符 y 表示一片黄叶。
出于美观整齐的考虑，小扣想要将收藏集中树叶的排列调整成「红、黄、红」三部分。每部分树叶数量可以不相等，但均需大于等于 1。每次调整操作，小扣可以将一片红叶替换成黄叶或者将一片黄叶替换成红叶。请问小扣最少需要多少次调整操作才能将秋叶收藏集调整完毕。

示例 1：

输入：leaves = “rrryyyrryyyrr”

输出：2

解释：调整两次，将中间的两片红叶替换成黄叶，得到 “rrryyyyyyyyrr”

示例 2：

输入：leaves = “ryr”

输出：0

解释：已符合要求，不需要额外操作

提示：

3 <= leaves.length <= 10^5
leaves 中只包含字符 ‘r’ 和字符 ‘y’

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/UlBDOe
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

最近忙着自闭（x）

解法动态规划，题解有时间再回来写（咕咕咕

2 - 771. 宝石与石头（简单）

给定字符串J 代表石头中宝石的类型，和字符串 S代表你拥有的石头。 S 中每个字符代表了一种你拥有的石头的类型，你想知道你拥有的石头中有多少是宝石。

J 中的字母不重复，J 和 S中的所有字符都是字母。字母区分大小写，因此”a”和”A”是不同类型的石头。

示例 1:

输入: J = “aA”, S = “aAAbbbb”
输出: 3
示例 2:

输入: J = “z”, S = “ZZ”
输出: 0
注意:

S 和 J 最多含有50个字母。
J 中的字符不重复。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/jewels-and-stones
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

用一个数组来保存有的宝石再遍历石头即可

因为是字符型，方便起见可以直接用一个128大小的数组来储存信息

构造代码如下：

int numJewelsInStones(char * J, char * S)
{
    char map[128] = {0};
    int num = 0;
    while(*J)
    {
        if(!(map[*J]))
            map[*J] = 1;
        J++;
    }
    printf("\n");
    while(*S)
    {
        if((map[*S]))
            num++;
        S++;
    }
    return num;
}

![KE97BAWWD__F`_X6X__``79.png](https://i.loli.net/2020/10/03/fGq8SYicjhrBIeN.png)

3 - 1. 两数之和（简单）

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那两个整数，并返回他们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素不能使用两遍。

示例:

给定 nums = [2, 7, 11, 15], target = 9

因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/two-sum
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

~~不忘初心牢记使命~~

是Leetcode的第一题呢

暴力枚举即可

构造代码如下：

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* twoSum(int* nums, int numsSize, int target, int* returnSize)
{
    int * retn = (int*) malloc(sizeof(int)*2);
    *returnSize = 2;
    for(int i=0;i<numsSize;i++)
    {
        for(int j=i+1;j<numsSize;j++)
        {
            if(nums[i] + nums[j] == target)
            {
                retn[0] = i;
                retn[1] = j;
                return retn;
            }
        }
    }
    return retn;
}

![R`X_RZK1I6_HG7_PV81~RNB.png](https://i.loli.net/2020/10/03/f8VGlqdrtjUIRsO.png)

4 - 2. 两数相加（中等）

给出两个非空的链表用来表示两个非负的整数。其中，它们各自的位数是按照逆序的方式存储的，并且它们的每个节点只能存储一位数字。

如果，我们将这两个数相加起来，则会返回一个新的链表来表示它们的和。

您可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例：

输入：(2 -> 4 -> 3) + (5 -> 6 -> 4)
输出：7 -> 0 -> 8
原因：342 + 465 = 807

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/add-two-numbers
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

呐，梦开始的地方呢。

解法：模拟法

模拟常规的加法过程即可

需要注意的是原结点的空间是可被复用的

时间复杂度：

需要遍历max(m,n)个结点（其中m为l1长度，n为l2长度），故时间复杂度为O(MAX(M,N))

空间复杂度：

只需要临时变量的常数空间，故空间复杂度为O(1)

构造代码如下：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */


struct ListNode* addTwoNumbers(struct ListNode* l1, struct ListNode* l2)
{
    if(!l1)
        return l2;
    if(!l2)
        return l1; 
    struct ListNode * tail, *retn = l1;
    int plus = 0;
    while(l1 && l2)
    {
        l1->val += l2->val + plus;
        plus = l1->val / 10;
        l1->val %= 10;
        tail = l1;
        l1 = l1->next;
        l2 = l2->next;
    }
    while(l1)
    {
        l1->val += plus;
        plus = l1->val / 10;
        l1->val %= 10;
        tail = l1;
        l1 = l1->next;
    }
    if(l2)
        tail->next = l2;
    while(l2)
    {
        l2->val += plus;
        plus = l2->val / 10;
        l2->val %= 10;
        tail = l2;
        l2 = l2->next;
    }
    if(plus)
    {
        tail->next = (struct ListNode *) malloc(sizeof(struct ListNode));
        tail->next->val = plus;
        tail->next->next = NULL;
    }
    return retn;
}

5 - 18. 四数之和（中等）

给定一个包含 n 个整数的数组 nums 和一个目标值 target，判断 nums 中是否存在四个元素 a，b，c 和 d ，使得 a + b + c + d 的值与 target 相等？找出所有满足条件且不重复的四元组。

注意：

答案中不可以包含重复的四元组。

示例：

给定数组 nums = [1, 0, -1, 0, -2, 2]，和 target = 0。

满足要求的四元组集合为：
[
[-1, 0, 0, 1],
[-2, -1, 1, 2],
[-2, 0, 0, 2]
]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/4sum
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

双指针哈希，留周末再写解法了

6 - 834. 树中距离之和（困难）

给定一个无向、连通的树。树中有 N 个标记为 0…N-1 的节点以及 N-1 条边。

第 i 条边连接节点 edges[i][0] 和 edges[i][1] 。

返回一个表示节点 i 与其他所有节点距离之和的列表 ans。

示例 1:

输入: N = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
输出: [8,12,6,10,10,10]
解释:
如下为给定的树的示意图：
0
/
1 2
/|
3 4 5

我们可以计算出 dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
也就是 1 + 1 + 2 + 2 + 2 = 8。因此，answer[0] = 8，以此类推。
说明: 1 <= N <= 10000

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/sum-of-distances-in-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

动态规划，周末写解法，最近忙的很

7 - 75. 颜色分类（中等）

给定一个包含红色、白色和蓝色，一共 n 个元素的数组，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

此题中，我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

注意:
不能使用代码库中的排序函数来解决这道题。

示例:

输入: [2,0,2,1,1,0]
输出: [0,0,1,1,2,2]
进阶：

一个直观的解决方案是使用计数排序的两趟扫描算法。
首先，迭代计算出0、1 和 2 元素的个数，然后按照0、1、2的排序，重写当前数组。
你能想出一个仅使用常数空间的一趟扫描算法吗？

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/sort-colors
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

因为只需要排序三种颜色，故考虑将数组分成三块，两趟遍历，第一趟把所有的0放在前面，第二趟把所有的1放在中间即可，在交换的过程中2自然会全部堆到末尾

时间复杂度：

最坏情况下两趟完整遍历，最好情况下遍历一趟，时间复杂度为O(N)

空间复杂度：

只需要常数级别的额外空间，故空间复杂度为O(1)

构造代码如下：

void sortColors(int* nums, int numsSize)
{
    int temp;
    for(int i=0;i<numsSize;i++)
    {
        for(int j=0;j<numsSize;j++)
        {
            if(nums[i] < nums[j])
            {
                temp = nums[i];
                nums[i] = nums[j];
                nums[j] = temp;
            }
        }
    }
}

8 - 344. 反转字符串（简单）

编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。

不要给另外的数组分配额外的空间，你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。

你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。

示例 1：

输入：[“h”,”e”,”l”,”l”,”o”]
输出：[“o”,”l”,”l”,”e”,”h”]
示例 2：

输入：[“H”,”a”,”n”,”n”,”a”,”h”]
输出：[“h”,”a”,”n”,”n”,”a”,”H”]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/reverse-string
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

原地交换即可

构造代码如下：

void reverseString(char* s, int sSize)
{
    char temp;
    int len = sSize/2;
    for(int i=0;i<len;i++)
    {
        temp=s[i];
        s[i]=s[sSize-i-1];
        s[sSize-i-1]=temp;
    }

}

9 - 141. 环形链表（简单）

给定一个链表，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回 true 。否则，返回 false 。

进阶：

你能用 O(1)（即，常量）内存解决此问题吗？

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。
示例 2：

输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。
示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

提示：

链表中节点的数目范围是 [0, 104]
-105 <= Node.val <= 105
pos 为 -1 或者链表中的一个有效索引。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/linked-list-cycle
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解法一：快慢指针

老快慢指针人了，只要链表中存在环那么在遍历过程中步长不一的快慢指针肯定会相遇

构造代码如下：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
bool hasCycle(struct ListNode *head) 
{
    if(!head)
        return false;
    struct ListNode * ptr1 = head, *ptr2 = head->next;
    while(ptr1 && ptr2)
    {
        if(ptr1 == ptr2)
            return true;
        ptr1 = ptr1->next;
        ptr2 = ptr2->next;
        if(!ptr2)
            break;
        ptr2 = ptr2->next;
    }
    return false;
}

解法二：利用题目数据范围漏洞

题目保证结点数量小于10000，那么只要遍历能循环超过10000次，链表中就必定存在回路

构造代码如下：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
bool hasCycle(struct ListNode *head) 
{
    int n = 0;
    while(head)
    {
        head = head->next;
        n++;
        if(n > 10000)
            return true;
    }
    return false;
}

10 - 142. 环形链表 II（中等）

给定一个链表，返回链表开始入环的第一个节点。如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。

说明：不允许修改给定的链表。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：tail connects to node index 1
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

输入：head = [1,2], pos = 0
输出：tail connects to node index 0
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：no cycle
解释：链表中没有环。

进阶：
你是否可以不用额外空间解决此题？

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/linked-list-cycle-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解法一：哈希表

用一个表收集已经遍历过的结点，每遍历过一个结点看这个结点是否在表内即可

当然，每次都要在表内寻找结点，时间复杂度最坏是O(N^2)

构造代码如下：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode *detectCycle(struct ListNode *head) 
{
    if(!head || !head->next)
        return NULL;
    
    struct ListNode * map[10000];
    int index = 0;
    while(head)
    {
        for(int i=0;i<index;i++)
        {
            if(head == map[i])
                return head;
        }
        map[index++] = head;
        head = head->next;
    }
    return NULL;
}

运行时间十分惨不忍睹

解法二：快慢指针

我们可以用步长分别为1、2的两个指针遍历该链表，思考如下事实：

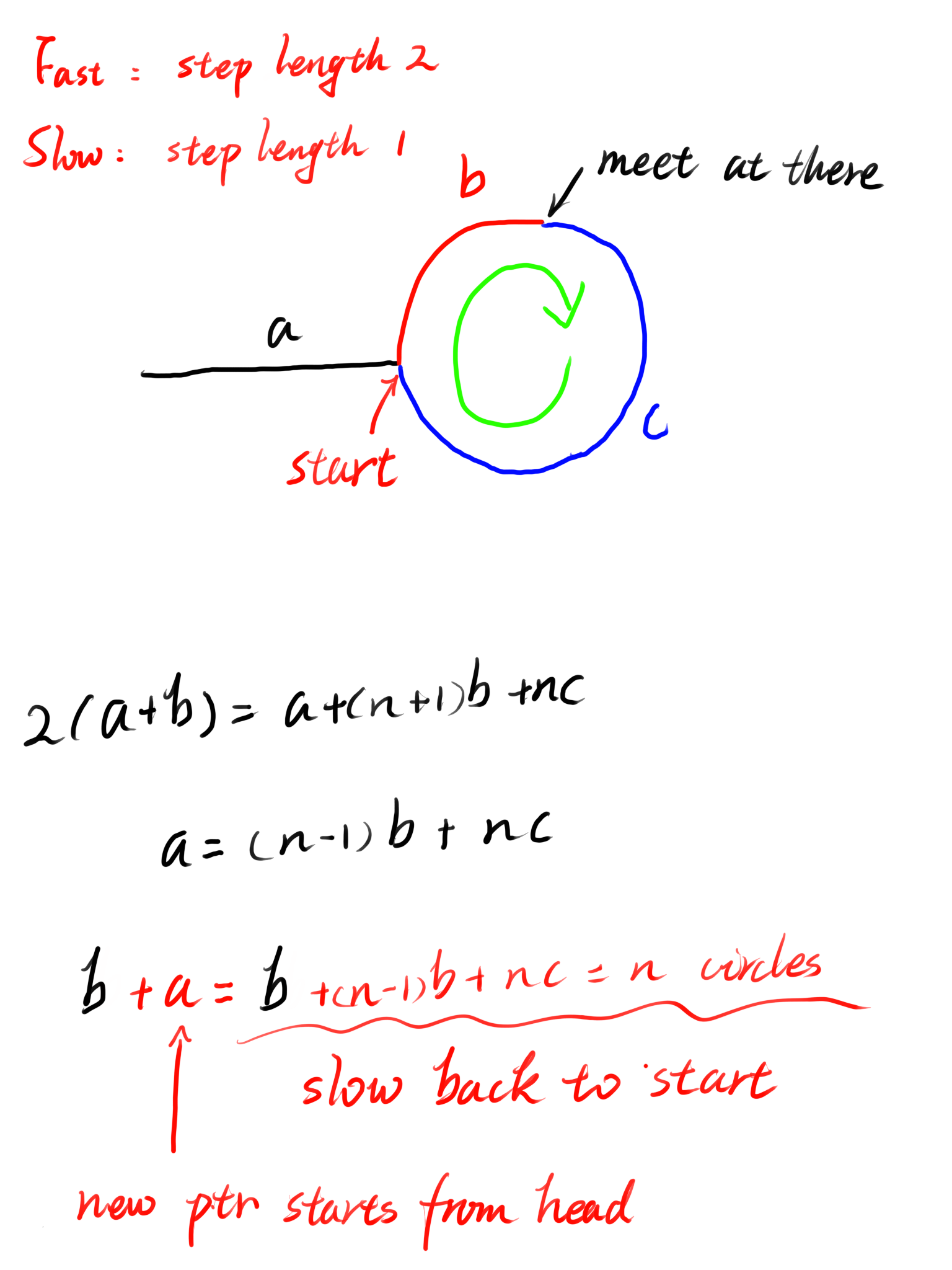
当快慢指针相遇后，慢指针从环的起始点走了距离b，若是从该时刻开始有一个指针从链表头与慢指针同步长遍历，当两指针相遇时，两个指针分别都走了距离a，此时慢指针总共从环的起始点走了a+b = n*b + n*c 的距离，刚好回到起始点，这样我们就找到环的起始点了

构造代码如下：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode *detectCycle(struct ListNode *head) 
{
    if(!head || !head->next)
        return NULL;
    
    struct ListNode * slow_ptr = head, *fast_ptr = head->next;
    while(slow_ptr && fast_ptr)
    {
        slow_ptr = slow_ptr->next;
        fast_ptr = fast_ptr->next;
        if(!fast_ptr)
            break;
        fast_ptr = fast_ptr->next;
        if(slow_ptr == fast_ptr)
        {
            slow_ptr = slow_ptr->next;
            struct ListNode * ptr = head;
            while(ptr != slow_ptr)
            {
                ptr = ptr->next;
                slow_ptr = slow_ptr->next;                
            }
            return ptr;
        }
    }
    return NULL;
}

11 - 416. 分割等和子集（中等）

给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

注意:

每个数组中的元素不会超过 100
数组的大小不会超过 200
示例 1:

输入: [1, 5, 11, 5]

输出: true

解释: 数组可以分割成 [1, 5, 5] 和 [11].

示例 2:

输入: [1, 2, 3, 5]

输出: false

解释: 数组不能分割成两个元素和相等的子集.

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/partition-equal-subset-sum
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

DP，01背包变种，题解先咕咕咕（

12 - 530. 二叉搜索树的最小绝对差（简单）

给你一棵所有节点为非负值的二叉搜索树，请你计算树中任意两节点的差的绝对值的最小值。

示例：

输入：

1

3
/
2

输出：
1

解释：
最小绝对差为 1，其中 2 和 1 的差的绝对值为 1（或者 2 和 3）。

提示：

树中至少有 2 个节点。
本题与 783 https://leetcode-cn.com/problems/minimum-distance-between-bst-nodes/ 相同

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/minimum-absolute-difference-in-bst
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解法：深度优先搜索 + 中序遍历

因为是二叉搜索树，所以当进行中序遍历时肯定会按照从小到大的结点进行遍历

最小绝对差肯定出现在相邻值结点中，这里就不再过多赘叙了

构造代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
int ans = 0xffff;
int pre = -1;

void dfs(struct TreeNode* root)
{
    if(!root)
        return ;
    dfs(root->left);
    if(pre == -1)
        pre = root->val;
    else
    {
        ans = (root->val - pre) < ans ? (root->val - pre) : ans;
        pre = root->val;
    }
    dfs(root->right);
}

int getMinimumDifference(struct TreeNode* root)
{
    pre = -1;
    ans = 0xffff;
    dfs(root);
    return ans;
}

13 - 24.两两交换链表中的节点（中等）

给定一个链表，两两交换其中相邻的节点，并返回交换后的链表。

你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

示例:

给定 1->2->3->4, 你应该返回 2->1->4->3.

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/swap-nodes-in-pairs
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

很简单的一个交换结点的题，两两交换即可

构造代码如下：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */


struct ListNode* swapPairs(struct ListNode* head)
{
    if(!head || !head->next)
        return head;
    struct ListNode * temp, *temp2 = head->next->next, *temp3 = (struct ListNode*) malloc(sizeof(struct ListNode)), *retn = head->next;
    temp3->next = head;
    while(head)
    {
        if(!head->next)
            break;
        temp2 = head->next->next;
        temp = head->next;
        temp3->next = temp;
        temp->next = head;
        head->next = temp2;
        temp3 = head;
        head = temp2;
    }
    return retn;
}

14 - 1002. 查找常用字符（简单）

给定仅有小写字母组成的字符串数组 A，返回列表中的每个字符串中都显示的全部字符（包括重复字符）组成的列表。例如，如果一个字符在每个字符串中出现 3 次，但不是 4 次，则需要在最终答案中包含该字符 3 次。

你可以按任意顺序返回答案。

示例 1：

输入：[“bella”,”label”,”roller”]
输出：[“e”,”l”,”l”]
示例 2：

输入：[“cool”,”lock”,”cook”]
输出：[“c”,”o”]

提示：

1 <= A.length <= 100
1 <= A[i].length <= 100
A[i][j] 是小写字母

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/find-common-characters
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

直接一个个数即可

构造代码如下：

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
char ** commonChars(char ** A, int ASize, int* returnSize)
{
    char ** retn = (char**)malloc(sizeof(void*) * 100);
    int ** count = (int**)calloc(sizeof(int*), 100);
    for(int i=0;i<100;i++)
        count[i] = (int*)calloc(sizeof(int), 30);
    *returnSize = 0;
    for(int i=0;i<ASize;i++)
    {
        char *ptr = A[i];
        for(int j=0;ptr[j];j++)
            count[i][ptr[j]-'a']++;
    }
    for(int i=0;i<26;i++)
    {
        bool flag = true;
        int min = 0xffff;
        for(int j=0;j<ASize;j++)
        {
            if(count[j][i] == 0)
            {
                flag = false;
                break;
            }
            min = min > count[j][i] ? count[j][i] : min;
        }
        if(flag)
        {
            for(int j=0;j<min;j++)
            {
                retn[*returnSize] = (char*)malloc(sizeof(char)*2);
                retn[*returnSize][0] = 'a' + i;
                retn[(*returnSize)++][1] = '\0';
            }
        }
    }
    return retn;
}

![7RM_2__VRFRFEI`8__F5YZW.png](https://i.loli.net/2020/10/14/Hu76mRdEKPnQY1b.png)

15 - 116. 填充每个节点的下一个右侧节点指针（中等）

给定一个完美二叉树，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例：

输入：{“$id”:”1”,”left”:{“$id”:”2”,”left”:{“$id”:”3”,”left”:null,”next”:null,”right”:null,”val”:4},”next”:null,”right”:{“$id”:”4”,”left”:null,”next”:null,”right”:null,”val”:5},”val”:2},”next”:null,”right”:{“$id”:”5”,”left”:{“$id”:”6”,”left”:null,”next”:null,”right”:null,”val”:6},”next”:null,”right”:{“$id”:”7”,”left”:null,”next”:null,”right”:null,”val”:7},”val”:3},”val”:1}

输出：{“$id”:”1”,”left”:{“$id”:”2”,”left”:{“$id”:”3”,”left”:null,”next”:{“$id”:”4”,”left”:null,”next”:{“$id”:”5”,”left”:null,”next”:{“$id”:”6”,”left”:null,”next”:null,”right”:null,”val”:7},”right”:null,”val”:6},”right”:null,”val”:5},”right”:null,”val”:4},”next”:{“$id”:”7”,”left”:{“$ref”:”5”},”next”:null,”right”:{“$ref”:”6”},”val”:3},”right”:{“$ref”:”4”},”val”:2},”next”:null,”right”:{“$ref”:”7”},”val”:1}

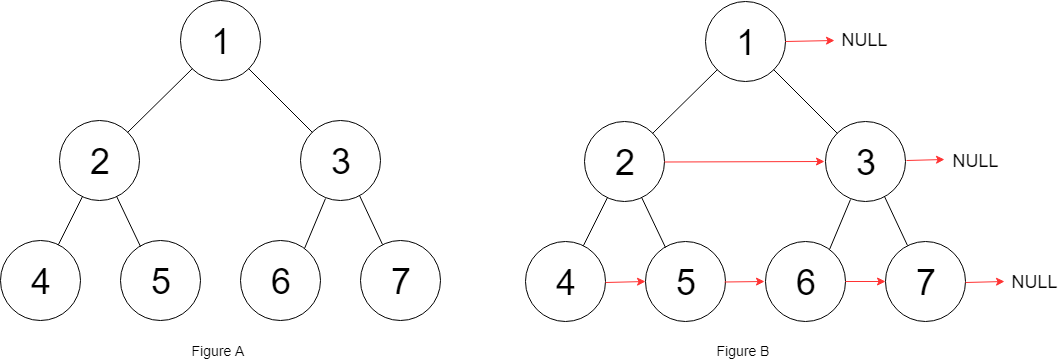
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。

提示：

你只能使用常量级额外空间。
使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/populating-next-right-pointers-in-each-node
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

注：本题和2020.9.28的每日一题几乎完全一样

解法一：层次遍历

大致过程如下图

时间复杂度：

由于每个结点都要遍历一次，故时间复杂度为O(N)

空间复杂度：

由于没有使用到额外的空间，故空间复杂度为O(1)

构造代码如下：

/**
 * Definition for a Node.
 * struct Node {
 *     int val;
 *     struct Node *left;
 *     struct Node *right;
 *     struct Node *next;
 * };
 */

struct Node * last_node, *next_start;

void connectList(struct Node * node)
{
    if(last_node)
    {
        last_node->next = node;
    }
    if(!next_start)
    {
        next_start = node;
    }
    last_node = node;
}

struct Node* connect(struct Node* root) 
{
	if(!root)
        return NULL;
    struct Node *start = root;
    while(start)
    {
        last_node = NULL, next_start = NULL;
        while(start)
        {
            if(start->left)
                connectList(start->left);
            if(start->right)
                connectList(start->right);
            start = start->next;
        }
        start = next_start;
    }
    return root;
}