arttnba3's old blog

- arttnba3的垃圾堆积处 -

0%

【OJ-0x0002-Leetcode】栈部分write up by arttnba3

Posted on Edited on In

0x00.绪论

栈（stack）是在任何的数据结构课本当中都会花一定篇幅来讲述的数据结构之一，作为一种抽象数据结构，无论是在算法应用（逆波兰表达式等）、计组原理（函数调用栈等）还是在安全领域（栈溢出等）都能见到这一抽象数据结构的身影。

上一篇关于Leetcode的博文里我们刷了简单线性表——单向链表的有关题目，那么这一次来刷一刷受限线性表——栈的有关题目叭2333333.

注：这个绪论是在半夜写的，可能我其实还没开始做题，如果你看到文章字数不到一千字的话可以先🦄住等后续的更新XD

注2：当晚回来打自己脸，写完绪论之后马上肝了几道题23333

注3：出于一些奇怪的原因，我会优先选择面试题

注4：点击标题可以直接进入原题网址

最后更新日期：2020.9.6

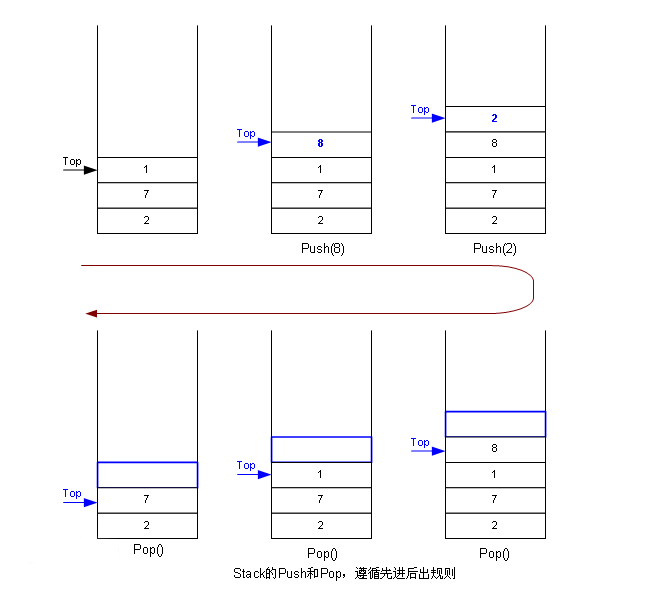
pre.栈的简单构造形式

我们都知道栈是一种受限线性表——后进先出表（Last In First Out，LIFO），我们常常喜欢使用“将一个元素压入栈中”的说法，在这个受限线性表中，最先进去的元素会被压在最下层，后面进来的元素会一层一层地堆叠起来，而一个元素若是想要出去，则只能“原路返回”：先让压在它上面的元素先逐一出去后，自己才能出去。

栈的构造大概如下图所示：

image.png

在这里我们可以注意到，我们在访问栈时，永远只能直接访问栈顶元素。我们可以联想到在内存管理中我们的stack pointer是永远指向栈帧（stack frame）的栈顶的。（好像有点扯远了XD

通常情况下，我们可以选择使用一个数组来模拟一个栈，并配上一个配套的指向栈顶的指针，这也是最简单的实现一个栈的形式。

1
2
int stack[stack_size];
int top = -1;

我们同样想到，作为一个受限线性表，我们可以使用一个链表结构来模拟一个栈，相比于数组结构而言其优势在于链表是动态的，不需要像数组那样提前额外地占用过多的内存空间

1
2
3
4
typedef struct stack{
    int value;
    struct stack* next;
}Stack;

0x01.难度：简单

0x00.有效的括号

给定一个只包括 ‘(‘，’)’，’{‘，’}’，’[‘，’]’ 的字符串，判断字符串是否有效。

有效字符串需满足：

1、左括号必须用相同类型的右括号闭合。
2、左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。

示例 1:

输入: “()”
输出: true
示例 2:

输入: “()[]{}”
输出: true
示例 3:

输入: “(]”
输出: false
示例 4:

输入: “([)]”
输出: false
示例 5:

输入: “{[]}”
输出: true

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/valid-parentheses
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

基本思路：

  • 逐个字符进行匹配

  • 遇到左括号：入栈

  • 遇到右括号：左括号出栈，与右括号进行匹配，若成功则进行下一轮匹配，失败则返回false

为了保证不溢出，我们首先选择使用链表构造栈，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
typedef struct stack{
    char value;
    struct stack* next;
}Stack;

bool isValid(char * str)
{
    if(str == NULL||str[0]=='\0')
        return true;
    int len = strlen(str);
    Stack *s = (Stack*)malloc(sizeof(Stack));
    s->value = -1;
    s->next = NULL;
    char ch;
    for(int i=0;i<len;i++)
    {
        ch = str[i];
        if(ch == '('||ch == '['||ch=='{')
        {
            Stack * temp = (Stack*)malloc(sizeof(Stack));
            temp->value = ch;
            temp->next = s;
            s = temp;
        }
        else if(ch == ')')
        {
            if(s->value!='(')
                return false;
            s = s->next;
        }
        else if(ch == ']')
        {
            if(s->value!='[')
                return false;
            s = s->next;
        }
        else if(ch == '}')
        {
            if(s->value!='{')
                return false;
            s = s->next;
        }
    }
    if(s->value!=-1)
        return false;
    return true;
}

image.png

空间上似乎不大行的样子，因为使用数组肯定是比使用链表要占用更少的空间

由于字符串的大小是可知的，故我们可以使用动态数组构造链表，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
bool isValid(char * str)
{
    if(str == NULL||str[0]=='\0')
        return true;
    int len = strlen(str);
    int top = -1;
    char * s = (char*)malloc(sizeof(char)*len+1);//prevent overflow
    char ch;
    for(int i=0;i<len;i++)
    {
        ch = str[i];
        if(ch == '('||ch == '['||ch=='{')
        {
            top++;
            s[top] = ch;
        }
        else if(ch == ')')
        {
            if(top == -1||s[top]!='(')
                return false;
            top--;
        }
        else if(ch == ']')
        {
            if(top == -1||s[top]!='[')
                return false;
            top--;
        }
        else if(ch == '}')
        {
            if(top == -1||s[top]!='{')
                return false;
            top--;
        }
    }
    if(top!=-1)
        return false;
    return true;
}

image.png

其实差的也不多嘛…

0x01.棒球比赛

你现在是棒球比赛记录员。
给定一个字符串列表，每个字符串可以是以下四种类型之一：

1.整数（一轮的得分）：直接表示您在本轮中获得的积分数。

  1. “+”（一轮的得分）：表示本轮获得的得分是前两轮有效 回合得分的总和。
  2. “D”（一轮的得分）：表示本轮获得的得分是前一轮有效 回合得分的两倍。
  3. “C”（一个操作，这不是一个回合的分数）：表示您获得的最后一个有效 回合的分数是无效的，应该被移除。

每一轮的操作都是永久性的，可能会对前一轮和后一轮产生影响。
你需要返回你在所有回合中得分的总和。

示例 1:

输入: [“5”,”2”,”C”,”D”,”+”]
输出: 30
解释:
第1轮：你可以得到5分。总和是：5。
第2轮：你可以得到2分。总和是：7。
操作1：第2轮的数据无效。总和是：5。
第3轮：你可以得到10分（第2轮的数据已被删除）。总数是：15。
第4轮：你可以得到5 + 10 = 15分。总数是：30。
示例 2:

输入: [“5”,”-2”,”4”,”C”,”D”,”9”,”+”,”+”]
输出: 27
解释:
第1轮：你可以得到5分。总和是：5。
第2轮：你可以得到-2分。总数是：3。
第3轮：你可以得到4分。总和是：7。
操作1：第3轮的数据无效。总数是：3。
第4轮：你可以得到-4分（第三轮的数据已被删除）。总和是：-1。
第5轮：你可以得到9分。总数是：8。
第6轮：你可以得到-4 + 9 = 5分。总数是13。
第7轮：你可以得到9 + 5 = 14分。总数是27。
注意：

输入列表的大小将介于1和1000之间。
列表中的每个整数都将介于-30000和30000之间。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/baseball-game
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

这是一道来自于《剑指Offer》的题目（简单到初中OIer都能做的题，说实话面试真的会考这种东西🐎，我暂且蒙在古里

求解的算法其实也很简单：

  • 遇到整数：入栈
  • 遇到操作数“+”：取栈顶元素的值与位于栈顶元素下方的元素的值，相加得到第三个元素，第三个元素入栈
  • 遇到操作数“D”：取栈顶元素的值*2，得到新元素，新元素入栈
  • 遇到操作数“C”：栈顶元素出栈

（说实话我感觉有点像求解前缀/后缀表达式的解法XD

因为操作数数量是已知的，故我们可以直接使用数组模拟栈，构造代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
int calPoints(char ** ops, int opsSize)
{
    int top = -1;
    int stack[opsSize+1];
    for(int i=0;i<opsSize;i++)
    {
        if(!strcmp(ops[i],"+"))
        {
            top++;
            stack[top] = stack[top-1]+stack[top-2];
        }
        else if(!strcmp(ops[i],"D"))
        {
            top++;
            stack[top] = stack[top-1]*2;
        }
        else if(!strcmp(ops[i],"C"))
        {
            top--;
        }
        else
        {
            top++;
            stack[top] = atoi(ops[i]);
        }
    }
    long long int result = 0;
    for(int i=0;i<=top;i++)
        result+=stack[i];
    return result;
}

image.png

0x02.下一个更大元素 I

给定两个 没有重复元素 的数组 nums1 和 nums2 ，其中nums1 是 nums2 的子集。找到 nums1 中每个元素在 nums2 中的下一个比其大的值。

nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在，对应位置输出 -1 。

示例 1:

输入: nums1 = [4,1,2], nums2 = [1,3,4,2].
输出: [-1,3,-1]
解释:
对于num1中的数字4，你无法在第二个数组中找到下一个更大的数字，因此输出 -1。
对于num1中的数字1，第二个数组中数字1右边的下一个较大数字是 3。
对于num1中的数字2，第二个数组中没有下一个更大的数字，因此输出 -1。
示例 2:

输入: nums1 = [2,4], nums2 = [1,2,3,4].
输出: [3,-1]
解释:
对于 num1 中的数字 2 ，第二个数组中的下一个较大数字是 3 。
对于 num1 中的数字 4 ，第二个数组中没有下一个更大的数字，因此输出 -1 。

提示：

nums1和nums2中所有元素是唯一的。
nums1和nums2 的数组大小都不超过1000。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/next-greater-element-i
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

num1是num2的子集，我们很容易想到：可以先在num2中对于每一个元素构造一个映射（哈希表），在遍历num1时只需要使用这个映射表即可

为了避免重复遍历，我们可以选择使用一个单调栈来短暂储存遍历中的元素，算法如下：

  • 任意元素入栈
  • 遇到比栈顶元素小的元素——入栈
  • 遇到比栈顶元素大的元素——栈内元素逐一出栈并构造映射，直到栈空或栈顶元素大于所遍历元素，此时该元素入栈
  • 遍历结束，栈内所有元素出栈并与-1构造映射

大小可知，还是选择简单的数组模拟栈，构造代码如下：

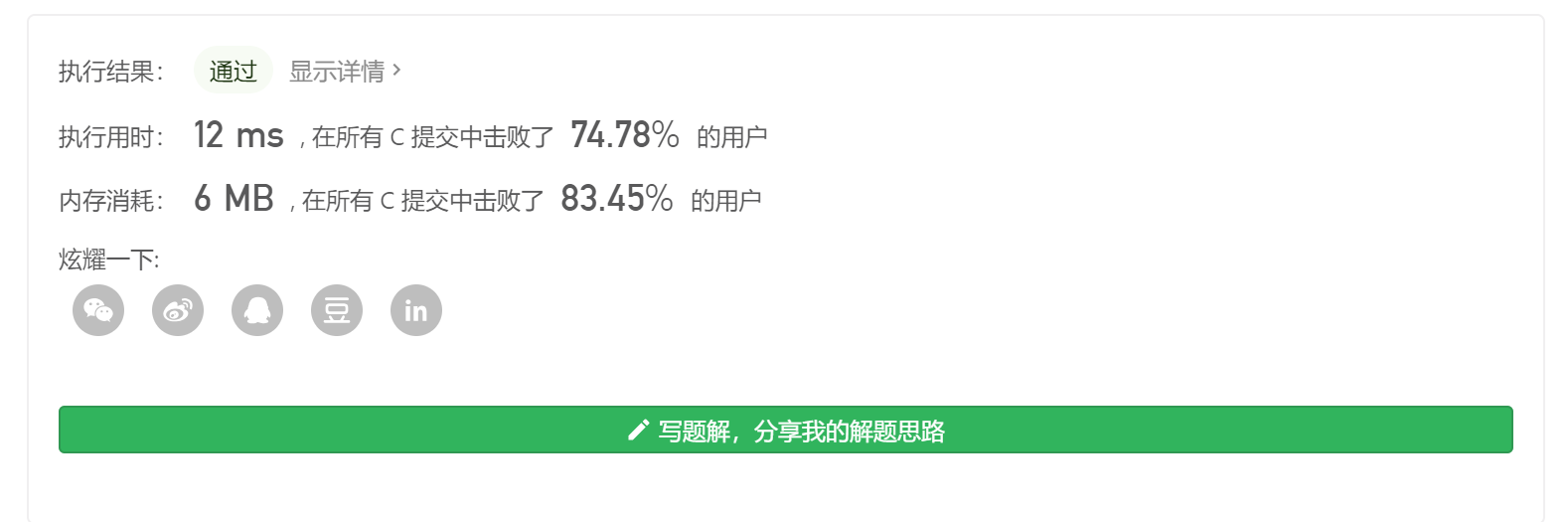
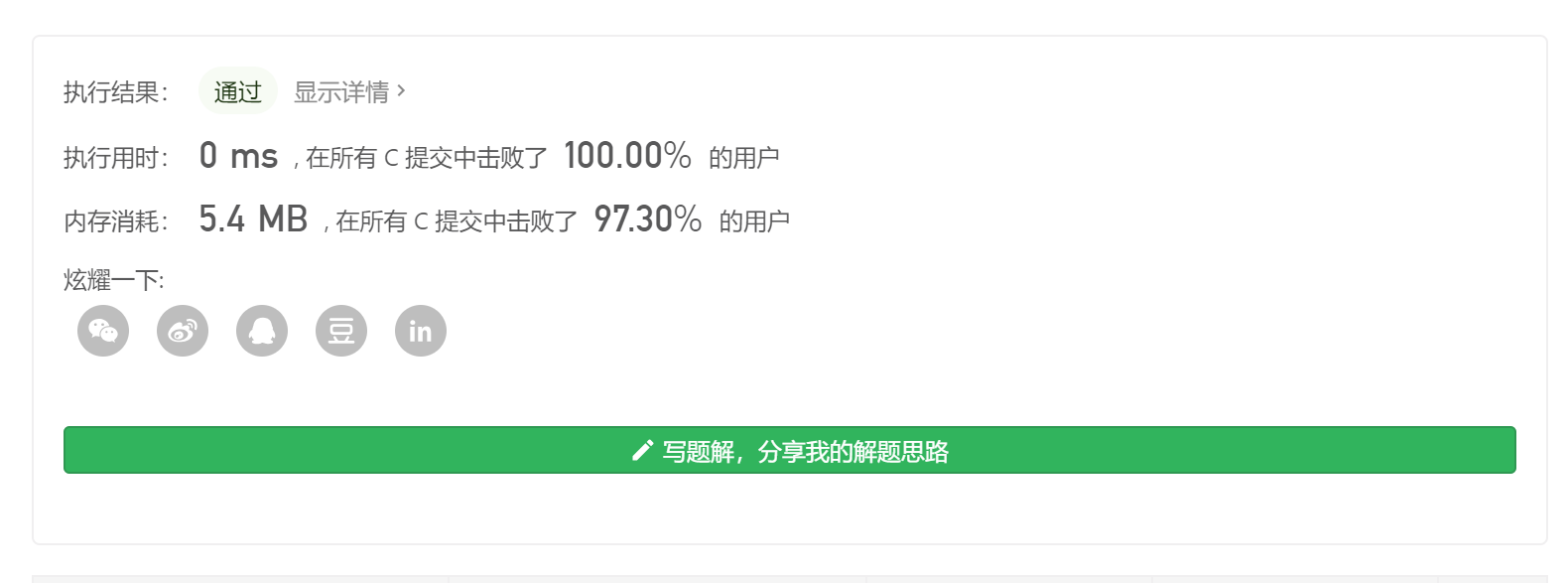
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* nextGreaterElement(int* nums1, int nums1Size, int* nums2, int nums2Size, int* returnSize)
{
    int table[nums2Size+5];
    int stack[nums2Size+5];
    int top = -1;
    for(int i=0;i<nums2Size;i++)
    {
        if(top == -1)
        {
            top++;
            stack[top] = i;//save the index instead of value
        }
        else
        {
            int _top=top;
            for(int j=0;j<=_top;j++)
            {
                if(nums2[i]>nums2[stack[top]])
                {
                    table[stack[top]] = nums2[i];
                    top--;
                }
                else
                    break;
            }
            top++;
            stack[top] = i;
        }
    }
    while(top!=-1)
    {
        table[stack[top]] = -1;
        top--;
    }
    int *arr = (int*)malloc(sizeof(int)*nums1Size);
    for(int i=0;i<nums1Size;i++)
    {
        int index=0;
        while(nums2[index]!=nums1[i])index++;
        arr[i]=table[index];
    }
    *returnSize = nums1Size;
    return arr;
}

结果如下，可以看到运行时间上不是那么的理想，因为我们在最后建立Nums1的映射时多次重复遍历，时间复杂度直接提升到O(N^2)

image.png

为了避免重复遍历，我们直接选择使用数组的值作为映射表的下标构造映射表数组进行取值，构造代码如下

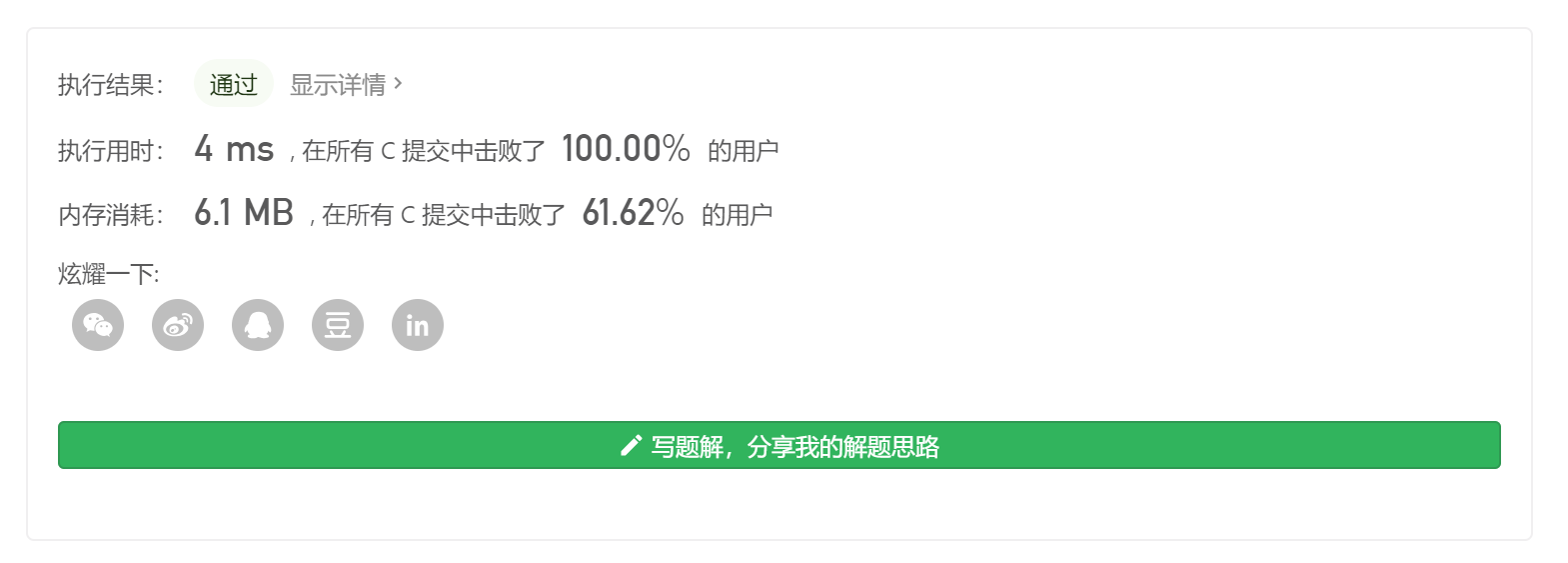
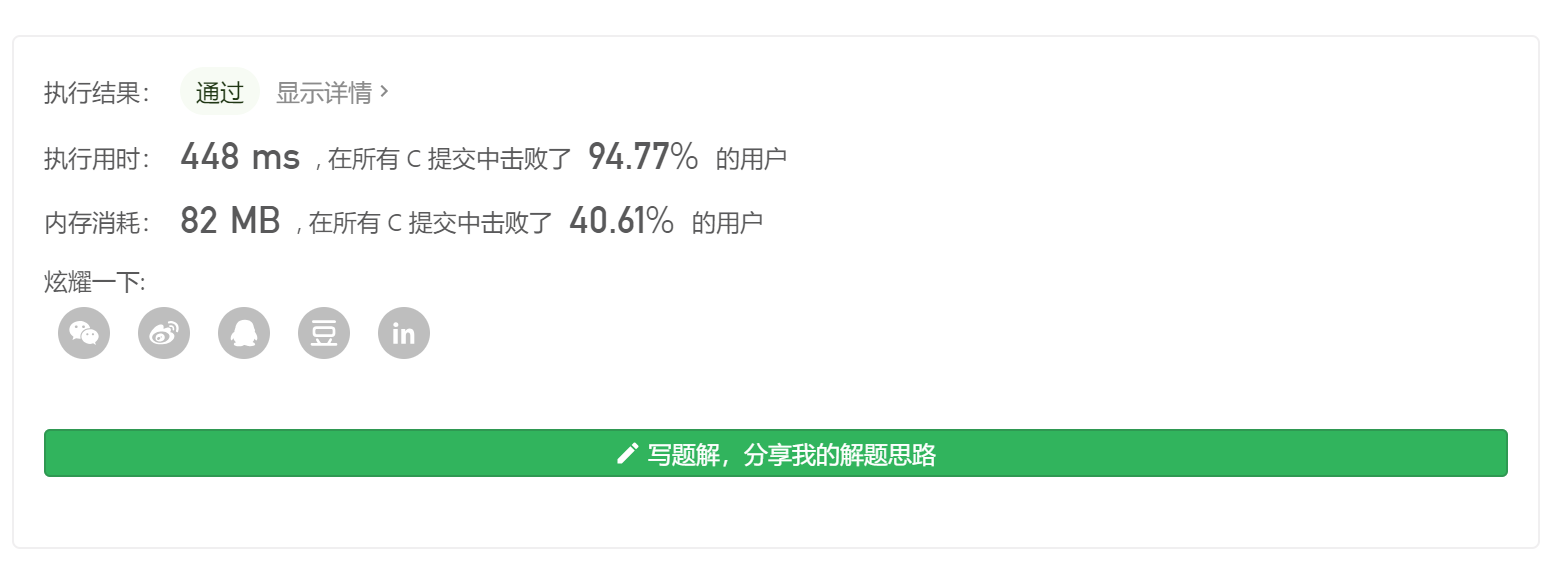
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* nextGreaterElement(int* nums1, int nums1Size, int* nums2, int nums2Size, int* returnSize)
{
    int max=0;
    for(int i=0;i<nums2Size;i++)
    {
        max = abs(nums2[i])>max?abs(nums2[i]):max;
    }
    int table[2*max+5];
    int stack[nums2Size+5];
    int top = -1;
    for(int i=0;i<nums2Size;i++)
    {
        while(top!=-1&&stack[top]<nums2[i])
        {
            table[max+stack[top]] = nums2[i];
            top--;
        }
        top++;
        stack[top] = nums2[i];
    }
    while(top!=-1)
    {
        table[stack[top]+max] = -1;
        top--;
    }
    int *arr = (int*)malloc(sizeof(int)*nums1Size);
    for(int i=0;i<nums1Size;i++)
    {
        arr[i]=table[nums1[i]+max];
    }
    *returnSize = nums1Size;
    return arr;
}

当然，由于我们所使用的映射表的大小取的是元素中绝对值最大的那一个作为大小，所以内存上会很吃亏，对于数值比较大的数据还是选择最初的解法

image.png

0x03.栈的最小值

请设计一个栈，除了常规栈支持的pop与push函数以外，还支持min函数，该函数返回栈元素中的最小值。执行push、pop和min操作的时间复杂度必须为O(1)。

示例：

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); –> 返回 -3.
minStack.pop();
minStack.top(); –> 返回 0.
minStack.getMin(); –> 返回 -2.

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/min-stack-lcci
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

大框架都给出来了，四舍五入相当于模板题

老链表人直接构造代码如下：

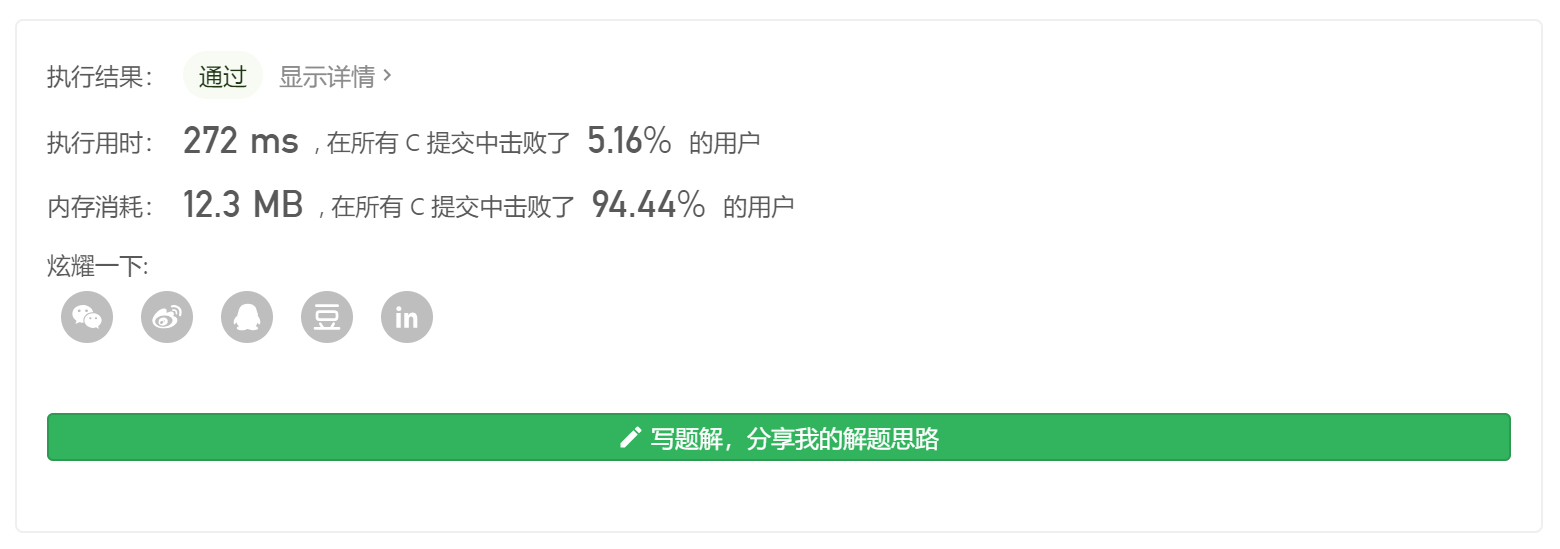
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
typedef struct Stack{
    int value;
    struct Stack * next;
} MinStack;

/** initialize your data structure here. */

MinStack* minStackCreate() 
{
    MinStack * stack = (MinStack*)malloc(sizeof(MinStack));
    stack->next = NULL;
    return stack;
}

void minStackPush(MinStack* obj, int x) 
{
    MinStack * stack = (MinStack*)malloc(sizeof(MinStack));
    stack->value = obj->value;
    stack->next = obj->next;
    obj->value = x;
    obj->next = stack;
}

void minStackPop(MinStack* obj) 
{
    if(obj->next==NULL)
        return;
    obj->value = obj->next->value;
    obj->next = obj->next->next;
}

int minStackTop(MinStack* obj) 
{
    if(obj->next==NULL)
        return 0;
    return obj->value;
}

int minStackGetMin(MinStack* obj) 
{
    int min = obj->value;
    obj = obj->next;
    while(obj->next!=NULL)
    {
        min = min<obj->value?min:obj->value;
        obj = obj->next;
    }
    return min;
}

void minStackFree(MinStack* obj) 
{
    MinStack* temp;
    while(obj->next!=NULL)
    {
        temp = obj;
        obj = obj->next;
        free(temp);
    }
    free(obj);
}

/**
 * Your MinStack struct will be instantiated and called as such:
 * MinStack* obj = minStackCreate();
 * minStackPush(obj, x);
 
 * minStackPop(obj);
 
 * int param_3 = minStackTop(obj);
 
 * int param_4 = minStackGetMin(obj);
 
 * minStackFree(obj);
*/

看得出来似乎时间复杂度太高了些，问题出在哪呢？

image.png

重新读一遍题目我们可以发现一个特殊的要求——push、pop、min的时间复杂度必须为O(1)，而我们遍历一遍栈检索最小值的过程的时间复杂度至少是O(N)

那么我们该如何优化呢？答案是使用另外一个栈来保存最小值，每当遇到比最小值小的元素入栈时将之也入最小值栈，该元素出栈时最小值栈也出栈，在需要取栈最小值时直接取该最小值栈的栈顶即可

故构造代码如下：

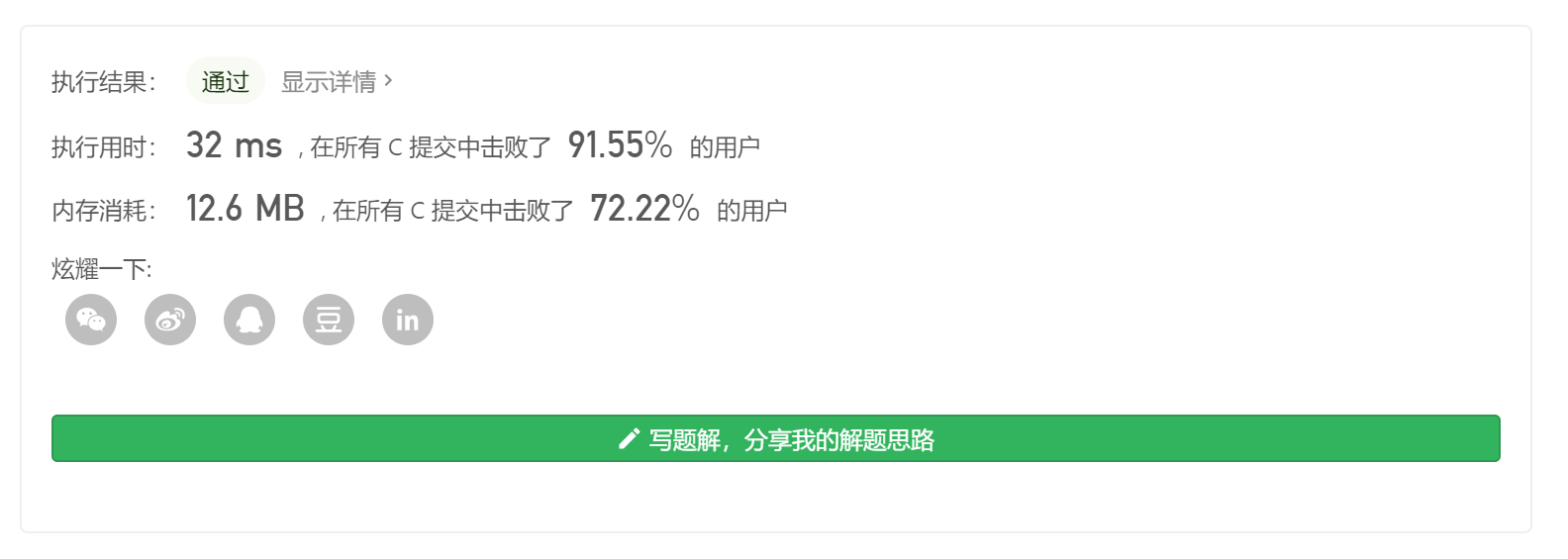
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
typedef struct Stack{
    int value;
    struct Stack * next;
} MinStack;
MinStack *min_stack;
/** initialize your data structure here. */

MinStack* minStackCreate() 
{
    MinStack * stack = (MinStack*)malloc(sizeof(MinStack));
    min_stack = (MinStack*)malloc(sizeof(MinStack));
    stack->next = NULL;
    min_stack->next = NULL;
    return stack;
}

void minStackPush(MinStack* obj, int x) 
{
    MinStack * stack = (MinStack*)malloc(sizeof(MinStack));
    stack->value = obj->value;
    stack->next = obj->next;
    obj->value = x;
    obj->next = stack;
    if(min_stack->next==NULL||x<=min_stack->value)
    {
        stack = (MinStack*)malloc(sizeof(MinStack));
        stack->value = min_stack->value;
        stack->next = min_stack->next;
        min_stack->value = x;
        min_stack->next = stack;
    }
}

void minStackPop(MinStack* obj) 
{
    if(obj->next==NULL)
        return;
    if(obj->value == min_stack->value&&min_stack->next!=NULL)
    {
        min_stack->value = min_stack->next->value;
        min_stack->next = min_stack->next->next;
    }
    obj->value = obj->next->value;
    obj->next = obj->next->next;
}

int minStackTop(MinStack* obj) 
{
    if(obj->next==NULL)
        return 0;
    return obj->value;
}

int minStackGetMin(MinStack* obj) 
{
    return min_stack->value;
}

void minStackFree(MinStack* obj) 
{
    MinStack* temp;
    while(obj->next!=NULL)
    {
        temp = obj;
        obj = obj->next;
        free(temp);
    }
    while(min_stack->next!=NULL)
    {
        temp = min_stack;
        min_stack = min_stack->next;
        free(temp);
    }
}

/**
 * Your MinStack struct will be instantiated and called as such:
 * MinStack* obj = minStackCreate();
 * minStackPush(obj, x);
 
 * minStackPop(obj);
 
 * int param_3 = minStackTop(obj);
 
 * int param_4 = minStackGetMin(obj);
 
 * minStackFree(obj);
*/

image.png

0x04.化栈为队

实现一个MyQueue类，该类用两个栈来实现一个队列。

示例：

MyQueue queue = new MyQueue();

queue.push(1);
queue.push(2);
queue.peek(); // 返回 1
queue.pop(); // 返回 1
queue.empty(); // 返回 false

说明：

你只能使用标准的栈操作 – 也就是只有 push to top, peek/pop from top, size 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。
假设所有操作都是有效的 （例如，一个空的队列不会调用 pop 或者 peek 操作）。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/implement-queue-using-stacks-lcci
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

据说是一道面试题（当然究竟面试会不会考这么简单的题我暂且蒙在古里

题目要求用两个栈来模拟一个队列，我们不难想到可以使一个栈in_stack负责处理push的元素，一个栈out_stack负责处理pop的元素

当元素需要出队时：

  • 检查out_stack是否为空
  • 若out_stack为空则将in_stack中元素逐一出栈并逐一入out_stack栈中，完成逆序栈构造
  • 将out_stack栈顶元素pop

故构造代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
typedef struct stack{
    int value;
    struct stack* next;
}Stack;

typedef struct 
{
    Stack * in_stack;
    Stack * out_stack;
} MyQueue;

/** Initialize your data structure here. */

MyQueue* myQueueCreate() 
{
    MyQueue * myQueue = (MyQueue*)malloc(sizeof(MyQueue));
    myQueue->in_stack = NULL;
    myQueue->out_stack = NULL;
    return myQueue;
}

/** Push element x to the back of queue. */
void myQueuePush(MyQueue* obj, int x) 
{
    Stack *s = (Stack*)malloc(sizeof(Stack));
    s->value = x;
    s->next = obj->in_stack;
    obj->in_stack = s;
}

/** Removes the element from in front of queue and returns that element. */
int myQueuePop(MyQueue* obj) 
{
    Stack * temp;
    if(obj->out_stack == NULL)
    {
        while(obj->in_stack!=NULL)
        {
            temp = obj->out_stack;
            obj->out_stack = obj->in_stack;
            obj->in_stack = obj->in_stack->next;
            obj->out_stack->next = temp;
        }
    }
    int n = obj->out_stack->value;
    temp = obj->out_stack;
    obj->out_stack = obj->out_stack->next;
    free(temp);
    return n;
}

/** Get the front element. */
int myQueuePeek(MyQueue* obj) 
{
    Stack * temp;
    if(obj->out_stack == NULL)
    {
        while(obj->in_stack!=NULL)
        {
            temp = obj->out_stack;
            obj->out_stack = obj->in_stack;
            obj->in_stack = obj->in_stack->next;
            obj->out_stack->next = temp;
        }
    }
    return obj->out_stack->value;
}

/** Returns whether the queue is empty. */
bool myQueueEmpty(MyQueue* obj) 
{
    if(obj->in_stack!=NULL||obj->out_stack!=NULL)
        return false;
    return true;
}

void myQueueFree(MyQueue* obj) 
{
    Stack*temp;
    while(obj->in_stack!=NULL)
    {
        temp = obj->in_stack;
        obj->in_stack = obj->in_stack->next;
        free(temp);
    }
    while(obj->out_stack!=NULL)
    {
        temp = obj->out_stack;
        obj->out_stack = obj->out_stack->next;
        free(temp);
    }
    free(obj);
}

/**
 * Your MyQueue struct will be instantiated and called as such:
 * MyQueue* obj = myQueueCreate();
 * myQueuePush(obj, x);
 
 * int param_2 = myQueuePop(obj);
 
 * int param_3 = myQueuePeek(obj);
 
 * bool param_4 = myQueueEmpty(obj);
 
 * myQueueFree(obj);
*/

image.png

0x05.剑指 Offer 09. 用两个栈实现队列

用两个栈实现一个队列。队列的声明如下，请实现它的两个函数 appendTail 和 deleteHead ，分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素，deleteHead 操作返回 -1 )

示例 1：

输入：
[“CQueue”,”appendTail”,”deleteHead”,”deleteHead”]
[[],[3],[],[]]
输出：[null,null,3,-1]
示例 2：

输入：
[“CQueue”,”deleteHead”,”appendTail”,”appendTail”,”deleteHead”,”deleteHead”]
[[],[],[5],[2],[],[]]
输出：[null,-1,null,null,5,2]
提示：

1 <= values <= 10000
最多会对 appendTail、deleteHead 进行 10000 次调用

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/yong-liang-ge-zhan-shi-xian-dui-lie-lcof
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

和这道题几乎一样的题（这种题都能上剑指offer么，蒟蒻OIer暂且蒙在古里），这一次给定了大小，为了省事我们选择使用数组来模拟栈

构造代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
typedef struct 
{
    int * in_stack;
    int * out_stack;
    int top_in;
    int top_out;
} CQueue;


CQueue* cQueueCreate() 
{
    CQueue *queue = (CQueue*)malloc(sizeof(CQueue));
    queue->top_in = -1;
    queue->top_out = -1;
    queue->in_stack = (int*)malloc(sizeof(int)*10005);
    queue->out_stack = (int*)malloc(sizeof(int)*10005);
    return queue;
}

void cQueueAppendTail(CQueue* obj, int value) 
{
    obj->top_in++;
    obj->in_stack[obj->top_in] = value;
}

int cQueueDeleteHead(CQueue* obj) 
{
    if(obj->top_in == -1&&obj->top_out == -1)
        return -1;
    if(obj->top_out == -1)
    {
        while(obj->top_in!=-1)
        {
            obj->top_out++;
            obj->out_stack[obj->top_out] = obj->in_stack[obj->top_in];
            obj->top_in--;
        }
    }
    obj->top_out--;
    return obj->out_stack[obj->top_out+1];
}

void cQueueFree(CQueue* obj) 
{
    free(obj->in_stack);
    free(obj->out_stack);
    free(obj);
}

/**
 * Your CQueue struct will be instantiated and called as such:
 * CQueue* obj = cQueueCreate();
 * cQueueAppendTail(obj, value);
 
 * int param_2 = cQueueDeleteHead(obj);
 
 * cQueueFree(obj);
*/

image.png

那么到这里为止，【简单】难度的offer题就刷完了

0x06.比较含退格的字符串

给定 S 和 T 两个字符串，当它们分别被输入到空白的文本编辑器后，判断二者是否相等，并返回结果。 # 代表退格字符。

注意：如果对空文本输入退格字符，文本继续为空。

示例 1：

输入：S = “ab#c”, T = “ad#c”
输出：true
解释：S 和 T 都会变成 “ac”。
示例 2：

输入：S = “ab##”, T = “c#d#”
输出：true
解释：S 和 T 都会变成 “”。
示例 3：

输入：S = “a##c”, T = “#a#c”
输出：true
解释：S 和 T 都会变成 “c”。
示例 4：

输入：S = “a#c”, T = “b”
输出：false
解释：S 会变成 “c”，但 T 仍然是 “b”。

提示：

1 <= S.length <= 200
1 <= T.length <= 200
S 和 T 只含有小写字母以及字符 ‘#’。

进阶：

你可以用 O(N) 的时间复杂度和 O(1) 的空间复杂度解决该问题吗？

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/backspace-string-compare
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

上电路分析课的时候闲着无聊（因为听不懂课（x））用iPad打的XD

遇到普通字符入栈，遇到'#'出栈一个字符即可

构造代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
bool backspaceCompare(char * S, char * T)
{
    char * s1 = malloc(sizeof(char)*205),*s2 = malloc(sizeof(char)*205);
    int len1 = 0, len2= 0;
    for(int i=0;S[i];i++)
    {
        if(S[i] == '#')
        {
            if(len1!=0)
                len1--;
        }
        else
            s1[len1++] = S[i];
    }
    for(int i=0;T[i];i++)
    {
        if(T[i] == '#')
        {
            if(len2!=0)
                len2--;
        }
        else
            s2[len2++] = T[i];
    }
    if(len1!=len2)
        return false;
    for(int i=0;i<len1;i++)
    {
        if(s1[i]!=s2[i])
            return false;
    }
    return true;
}

image.png

0x02.难度：中等

0x00.队列的最大值

请定义一个队列并实现函数 max_value 得到队列里的最大值，要求函数max_value、push_back 和 pop_front 的均摊时间复杂度都是O(1)。

若队列为空，pop_front 和 max_value 需要返回 -1

示例 1：

输入:
[“MaxQueue”,”push_back”,”push_back”,”max_value”,”pop_front”,”max_value”]
[[],[1],[2],[],[],[]]
输出: [null,null,null,2,1,2]
示例 2：

输入:
[“MaxQueue”,”pop_front”,”max_value”]
[[],[],[]]
输出: [null,-1,-1]

限制：

1 <= push_back,pop_front,max_value的总操作数 <= 10000
1 <= value <= 10^5

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/dui-lie-de-zui-da-zhi-lcof
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

同样是一道来自于剑指offer的题目，照抄之前的两个栈构建队列即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
typedef struct stack{
    int value;
    struct stack* next;
}Stack;

typedef struct 
{
    Stack * in_stack;
    Stack * out_stack;
} MaxQueue;


MaxQueue* maxQueueCreate() 
{
    MaxQueue * myQueue = (MaxQueue*)malloc(sizeof(MaxQueue));
    myQueue->in_stack = NULL;
    myQueue->out_stack = NULL;
    return myQueue;
}

int maxQueueMax_value(MaxQueue* obj) 
{
    if(obj->in_stack==NULL&&obj->out_stack==NULL)
        return -1;
    bool pd1=false,pd2=false;
    int max1,max2;
    Stack* temp1=obj->in_stack,*temp2=obj->out_stack;
    if(temp1!=NULL)
    {
        max1=temp1->value;
        pd1 = true;
    }
    if(temp2!=NULL)
    {
        max2=temp2->value;
        pd2 = true;
    }
    while(temp1!=NULL)
    {
        max1 = max1>temp1->value?max1:temp1->value;
        temp1 = temp1->next;
    }
    while(temp2!=NULL)
    {
        max2 = max2>temp2->value?max2:temp2->value;
        temp2 = temp2->next;
    }
    if(pd1&&pd2)
        return max1>max2?max1:max2;
    else if(pd1)
        return max1;
    else
        return max2;
}

void maxQueuePush_back(MaxQueue* obj, int value) 
{
    Stack *s = (Stack*)malloc(sizeof(Stack));
    s->value = value;
    s->next = obj->in_stack;
    obj->in_stack = s;
}

int maxQueuePop_front(MaxQueue* obj) 
{
    Stack * temp;
    if(obj->out_stack == NULL)
    {
        if(obj->in_stack==NULL)
            return -1;
        while(obj->in_stack!=NULL)
        {
            temp = obj->out_stack;
            obj->out_stack = obj->in_stack;
            obj->in_stack = obj->in_stack->next;
            obj->out_stack->next = temp;
        }
    }
    int n = obj->out_stack->value;
    temp = obj->out_stack;
    obj->out_stack = obj->out_stack->next;
    free(temp);
    return n;
}

void maxQueueFree(MaxQueue* obj) 
{
    Stack*temp;
    while(obj->in_stack!=NULL)
    {
        temp = obj->in_stack;
        obj->in_stack = obj->in_stack->next;
        free(temp);
    }
    while(obj->out_stack!=NULL)
    {
        temp = obj->out_stack;
        obj->out_stack = obj->out_stack->next;
        free(temp);
    }
}

/**
 * Your MaxQueue struct will be instantiated and called as such:
 * MaxQueue* obj = maxQueueCreate();
 * int param_1 = maxQueueMax_value(obj);
 
 * maxQueuePush_back(obj, value);
 
 * int param_3 = maxQueuePop_front(obj);
 
 * maxQueueFree(obj);
*/

image.png

咕了，后面有时间再继续做🕊🕊🕊

Welcome to my other publishing channels