arttnba3's old blog

- arttnba3的垃圾堆积处 -

0%

【算法浅析-0x02】Dijkstra算法浅析 by arttnba3

Posted on Edited on In

0x00.绪论

Dijkstra算法算是图论当中最为基础的算法之一，也是各类信息学竞赛（ Olympiad in Informatics ）当中各大图论算法的基础，碰巧今天的离散数学课刚好讲到了Dijkstra算法，所以作为一名蒟蒻·前OIer，今天就来简单讲讲什么是Dijkstra算法XD

不过我当年打OI的时候基本没怎么研究过图论，所以没出过啥成绩XD

0x01.什么是Dijkstra算法？

定义

迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959 年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。

百度百科：Dijkstra算法

戴克斯特拉算法设置了一顶点集合S，在集合中所有的顶点与源点s之间的最终最短路径权值均已确定。算法反复选择最短路径估计最小的点u∈V-S并将加入中。该算法常用于路由其他图算法的一个子模块

维基百科：戴克斯特拉算法

简单地说，Dijkstra算法就是：在正权图中使用贪心算法不断进行搜索从而求出最短路径的搜索算法

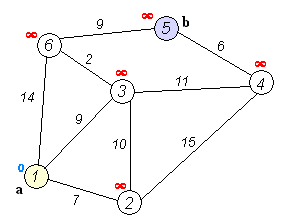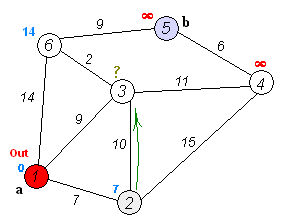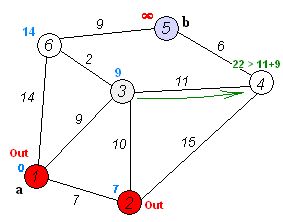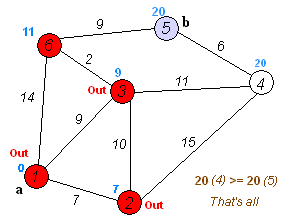
具体过程

在维基百科上有这样一张很经典的动图，很好地向我们演示了什么是Dijkstra算法：

c43291221c382a277596d38654993caf_Dijkstra_Animation.gif

从上面我们不难看出Dijkstra算法的整个过程：

  • 将每个点的权值（即起始点到达该点的距离）设置为∞

  • 从起始点出发，搜索距离其最近的点，将之纳入点集S

  • 搜索该最近点所能到达的所有未被占用点，对比【未被占用点原权值】与【该最近点权值+边权值】的大小，若后者较小则改写该未被占用点权值并记录路径

  • 不断重复第二、三步，直到所有点都被纳入点集S（即V-S= Ø，V为该图所有点的点集 ）即可得到出发点距离结束点的最短路径与最短距离

注意：第二步的第一次搜索恒为起始点本身，即将起始点纳入点集

以上即为基本的Dijkstra算法的整个过程，我们不难看出这一种不断搜索最短距离的过程其实是一种类似于贪心算法的思想，同时这样的一种路径结果记录的方法也有一定的动态规划的思想在内——到达被纳入点的最短路径已经是最优状态，无后效性，具有最优子结构

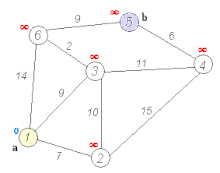
基本概念：图的表示

在图论当中我们常用一个二维矩阵来表示一个图，比如说上面动图中的那一张图:

image.png

我们可以使用下面这样的一个矩阵来表示（无向图）：
image.png

对于无向图而言，他的邻接矩阵一定会是对称的，在离散数学课上已经讲过，这里就不再多说了

我们不难看出，这样一个矩阵很像一个二维数组，因此我们可以使用一个二维数组（邻接矩阵）表示一张图：

1
int map[MAX][MAX];

但是毫无疑问地，随着图的越来越大，二维数组所占用的空间也会爆炸式增长（尤其是像OI那样动不动就10^8、10^9的），因此我们还需要更好的方法来表示一张图

对于图G=(V,E)(其中V为点集，E为边集)，我们也可以使用邻接表来表示一张有向图：

1
2
3
4
#include<vector>
using namespace std;
define edge pair<int, int>//始点到终点，可用于表示有向图
vector < pair < int, edge > > map;//点集与边集

当图为稀疏图、顶点较多，即图结构比较大时，更适宜选择邻接表作为存储结构。当图为稠密图、顶点较少时，或者不需要记录图中边的权值时，使用邻接矩阵作为存储结构较为合适。

代码实现

邻接矩阵版

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
#include<iostream>
using namespace std;
#define MAX 10000

void dijkstra(void);
void pathOut(int node);

int map[MAX][MAX]={0};//储存邻接矩阵
int node, start;//点数与起始点
int dist[MAX]={0};//起始点到各点最短距离
int path[MAX]={0};//到各点的最短路径，其中每个元素储存的是在到达该点的最短路径上该点的上一个点
bool visited[MAX]={0};//占用点的集合

int main(void)
{
    //freopen("input.txt","r",stdin);
    cout<<"Please enter the number of the nodes"<<endl;
    cin>>node;
    cout<<"please enter this maps\'s Adjacency Matrix"<<endl;
    for(int i=1;i<=node;i++)
    {
        for(int j=1;j<=node;j++)
        {
            cin>>map[i][j];
        }
    }
    cout<<"Please enter the start node: ";
    cin>>start;
    dijkstra();
    for(int i = 1;i<=node;i++)
    {    
        cout<<endl<<"distance to node "<<i<<" is "<<dist[i]<<" . The path is: ";
        pathOut(i);
    }
    return 0;
}

void dijkstra(void)//核心函数：Dijkstra，搜索出发点到各点的最短路径
{
    //初始化
    for(int i=1;i<=node;i++)
    {    
        dist[i] = MAX;//到各点距离设为∞
        visited[i] = false;//清空点集合
    }
    //将起始点纳入
    dist[start] = 0;
    visited[start] = true;
    path[start] = start;
    int best = start;
    //遍历各点
    for(int i=1;i<=node;i++)
    {
        int min = MAX;
        for(int j = 1;j<=node;j++)//寻找【距离起始点最近的点】
            if(!visited[j]&&dist[j]<min)//若该点未被占用且权值小于已知最近点权值
            {
                min = dist[j];//更新已知最近点距离
                best = j;//更新最近点
            }
        visited[best] = true;//将该点纳入集合
        for(int j=1;j<=node;j++)//遍历各点
            /*若
            * 该最近点能够到达j点
            * j点未被占用
            * 起始点到j点的距离 > 起始点到该最近点的距离 + 该最近点到j点的距离
            * 更新起始点到j点的距离 为 起始点到该最近点的距离 + 该最近点到j点的距离
            */
            if(map[best][j]!=0&&!visited[j]&&dist[j]>dist[best]+map[best][j])
            {    
                dist[j] = dist[best]+map[best][j];
                path[j] = best;
            }
    }
}

void pathOut(int node)//用来递归打印最短路径的函数
{
    if(path[node] != node)
    {
        pathOut(path[node]);
        cout<<" -> "<<node;
    }
    else
    {
        cout<<node;
    }
    
}

我们以基本概念中的图作为输入样例，选取点2为出发点：

image.png

得到如下结果：

image.png

对比原图，我们不难看出我们所得出的结果是正确的

邻接表

方便起见，我们假设起始点恒为点1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
//假设起始点为1
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
#define edge pair < int, int>
#define infinite 1145141919

vector < pair < int, edge > > G;
vector<int> key, rel;// 起始点到各点距离，到各点最短路径上该点的上一点
int node, edg;

void init_keys()//初始化各点权值为infinite
{
	key.resize(node);
	key[0]=0;//初始化起始点权值为0
	for(int i=1; i<node; i++)
	{
		key[i]=infinite;
	}
}

void dijkstra()
{
	rel.resize(node);
	int count=0;
	sort(G.begin(), G.end());//将各点按照点1（起始点）~末点进行排序
	while(count<edg)//遍历每一条边
	{
        //若【[起始点]到[[边count]上的起点]的权值 + 该边权值】 < 【[起始点]到[[边count]的终点]的权值】
		if((key[G[count].first]+G[count].second.second)<key[G[count].second.first])
		{
            //设 [起始点] 到[[边count]的终点] 的 最短路径上 [[边count]的终点] 的 [上一点] 为 [[边count]的起点]
			rel[G[count].second.first]=G[count].first;
            //设 【[起始点] 到[[边count]的终点] 的 权值】 为 【[起始点]到[[边count]的起点]的权值 + [边count]的权值】
			key[G[count].second.first]=key[G[count].first]+G[count].second.second;			
		}
		count++;
	};
}

int main()
{
    //freopen("input2.txt","r",stdin);
    int x, y, cost;
    cin>>node>>edg;
    for(int i=0; i<edg; i++)
    {
        cin>>x>>y>>cost;
        G.push_back(pair <int, edge>(x-1, edge(y-1, cost)));
    }
    init_keys();
    dijkstra();
    cout<<"Shortest path: \n 1 is ROOT\n";
    for(int i=1; i<node; i++)
    {
		cout<<"( "<<i+1<<", "<<rel[i]+1<<" )\n";
	}
	cout<<"Shortest path for? : ";
	cin>>x;
	cout<<"\nShortest path from 1 to "<<x<<" is "<<key[x-1];
    return 0;
}

优化：堆优化

咕了，下次再补

Welcome to my other publishing channels